Introduction
Legend has it that around 2200 BC, a turtle with an exceptionally unique shell crossed paths with King Yu of China one day as he was partaking in his daily walk along the Yellow River.

The order and configuration of the dots and squares fueled King Yu’s curiosity. As he analyzed the numbers in more detail, he noticed something about each column, row and main diagonals. Fill in the chart below with the number of dots in each square.
What Do You Notice? What Do You Wonder?
Use the drawing tools, text box or equation button to share your notices and wonders.
Magic Squares
This unique pattern on the turtle's shell is referred to as the Lo-Shu, a Magic Square that has been studied by mathematicians all over the world and placed on different stones and charms with an arrangement of dots very similar to the picture below.
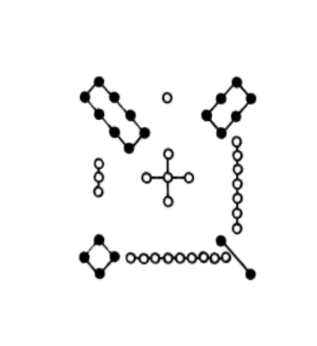
Fill in the chart below with the number of dots in each square.
What do you think the Magic Number is for this Magic Square? Check by Finding the Sum of all Rows, Columns, and Diagonals.
Can you fill in the missing numbers here to complete the magic squares below?
Extension
Albrecht Durer was a German renaissance artist who included a special magic square with fascinating properties in an engraving called Melencolia I. On top of sharing a Magic Sum of each row, column, and diagonal, each of the two by two squares in each of the four quadrants (top left square, top right square, bottom left square, bottom right square) share the magic sum.
What is the Magic Sum? Can you fill in this Durer Magic Square? There are 86 different ways to achieve the magic sum within the magic square. How many can you find?
When we subtract each number in the Durer Magic Square from , the result gives us a Complementary Magic Square, which holds the same properties of a Magic Square. Since this is a four by four Magic square, . Subtract each number in the Durer Magic from to create a complementary magic square?
References
Fults, J. (1974). Magic squares. LaSalle, Ill: Open Court,.
Pickover, C. (2002). The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across Dimensions. Princeton, New Jersey; Woodstock, Oxfordshire: Princeton University Press.
The Puzzle Universe A History of Mathematics in 315 Puzzles by Ivan Moscovich