Machine LearningNeural Networks
There is yet another way to build complex models out of more basic ones: composition. We can use outputs of one model as inputs of the next model, and we train the full composition to map training inputs to training outputs.
Using linear functions as our building blocks is a dead end:
Example
An affine function from to is a function of the form , where is an matrix and . Show that a composition of affine functions is affine.
Solution. We have , which is of the form (matrix times plus vector).
This example shows that composing affine functions does not yield any new functions. We will introduce nonlinearity by applying a fixed function componentwise after each affine map application. We call the activation function. The modern default activation to use is the ReLU function . We borrow some Julia syntax and write for the function which applies pointwise:
Given an affine map , we call the weight matrix and the bias vector.
Example
Suppose that and . Find , where is the ReLU activation function.
Solution. We have . Applying to each component yields . Finally, applying yields
We will use a diagram to visualize our neural net as a composition of maps. We include the sequence of alternating affine and activation maps, and we also include one final map which associates a real-valued cost with each output vector. Given a training observation , let's consider the cost (which measures squared distance from the vector output by the neural net and the desired vector ). Our goal will be to find values for the weights and biases which yield a small average value for as ranges over the set of training observations.
Definition
A neural network function is a composition of affine transformations and componentwise applications of a function .

The architecture of a neural network is the sequence of dimensions of the domains and codomains of its affine maps.
In principle, we have fully specified a neural network learner: given a set of training observations and a choice of architecture, we can ask for the weights and biases which minimize the average cost over the training observations. However, this is not the end of the story, for two reasons: neural net cost minimization is not a convex problem, and finding a global minimum is typically not feasible. Furthermore, even if the global minimum can be found, it is typically overfit. Therefore, building an effective neural net requires finessing not only the setup (architecture, choice of activation function, choice of cost function) but also the details of the optimization algorithm.
Neural networks are typically trained using stochastic gradient descent. The idea is to determine for each training observation the desired nudges to each weight and bias to reduce the cost for that observation. Rather than performing this calculation for every observation in the training set (which is, ideally, enormous), we do it for a randomly selected subset of the training data.
The main challenge in implementing stochastic gradient descent is the bookkeeping associated with all the nodes in the neural net diagram. We will use matrix differentiation to simplify that process. Let's begin by defining a neural net data type and writing some basic methods for it.
Example
Create data types in Julia to represent affine maps and neural net functions. Write an architecture method for neural nets which returns the sequence of dimensions of the domains and codomains of its affine maps.
Solution. We supply a NeuralNet with the sequence of affine maps, the activation function, and also the activation function's derivative. We write call methods for the AffineMap and NeuralNet types so they can be applied as functions to appropriate inputs. (One of these methods refers to a function we will define in the next example.)
using LinearAlgebra, StatsBase, Test
struct AffineMap
W::Matrix
b::Vector
end
struct NeuralNet
maps::Vector{AffineMap}
K::Function # activation function
K̇::Function # derivative of K
end
(A::AffineMap)(x) = A.W * x + A.b
(NN::NeuralNet)(x) = forwardprop(NN,x)[end]
architecture(NN::NeuralNet) = [[size(A.W,2) for A in NN.maps];
size(last(NN.maps).W,1)]Now we can set up an example neural network to use for tests later.
W₁ = [3.0 -4; -2 4] W₂ = [1.0 -1] b₁ = [1.0, -4] b₂ = [0.0]; K(x) = x > 0 ? x : 0 K̇(x) = x > 0 ? 1 : 0 NN = NeuralNet([AffineMap(W₁, b₁), AffineMap(W₂, b₂)], K, K̇)
Successively applying the maps in the neural network is called forward propagation.
Example
Write a Julia function forwardprop which calculates the sequence of vectors obtained by applying each successive map in the neural net (in other words, the vectors which are output from each map and input into the next one).
Solution. We store the sequence of values we obtain in an array called vectors. The very last map is the identity function rather than , so it must be handled separately.
function forwardprop(NN::NeuralNet,x)
activations = [x]
for (j,A) in enumerate(NN.maps)
push!(activations,A(activations[end]))
K = j < length(NN.maps) ? NN.K : identity
push!(activations,K.(activations[end]))
end
activations
end
activations = forwardprop(NN, [-2.0, -3])
@test activations == [[-2, -3], [7, -12], [7, 0], [7], [7]]To adjust the weights and biases of the neural net in a favorable direction, we want to compute for every node the derivative of the value in the cost node with respect to the value in node . The node which is easiest to compute the derivative for is the prediction vector node, since the only map between that node and the cost is .
More generally, given the derivative value for any particular node , we can calculate the derivative for the node immediately to its left, using the chain rule. A small change in the value at node induces a small change in the value at node (where denotes the map between and ). This change in turn induces a change in the cost value (where denotes the map from to the cost node). In other words, the net result of the small change is the product of the two derivative matrices and .
So we can work from right to left in the diagram and calculate the derivative values for all of the nodes. This is called backpropagation. We will just need to calculate the derivatives of the maps between adjacent nodes.
Example
- Find the derivative of with respect to .
- Find the derivative of (the map which applies pointwise).
- Find the derivative of , where is a matrix and is a vector.
Solution.
- The derivative of is
by the product rule.
- The derivative with respect to has th entry , which is equal to 0 if and if (where we're borrowing from physics the notation for the derivative of ). In other words, the derivative of with respect to is . (Here means "form a diagonal matrix with this vector's entries on the diagonal", the dot on top means "derivative", and the subscript dot means "apply componentwise".)
- The derivative of with respect to is .
Example
Write a Julia function backprop which calculates the for each node the derivative of the cost function with respect to the value at that node. In other words, calculate the derivative of the composition of maps between that node and the cost node at the end.
Solution. We can use all the derivatives we calculated in the previous example. We define functions which return the index of the th green node and the th purple node in the diagram, for convenience.
"Index of jth green node"
greennode(j) = 2j-1
"Index of jth purple node"
purplenode(j) = 2j
"""
Compute the gradient of each composition of maps from
an intermediate node to the final output.
"""
function backprop(NN::NeuralNet,activations,yᵢ)
y = activations[end]
grads = [2(y-yᵢ)']
for j in length(NN.maps) : -1 : 1
if j == length(NN.maps)
push!(grads, grads[end])
else
push!(grads, grads[end] *
Diagonal(NN.K̇.(activations[purplenode(j)])))
end
push!(grads, grads[end] * NN.maps[j].W)
end
reverse(grads)
end
gradients = backprop(NN, activations, [2.0])
@test gradients ==
[[30, -40]', [10, 0]', [10, -10]', [10]', [10]']With the derivative values computed for all of the nodes on the bottom row, we can calculate the derivative of the cost function with respect to the weights and biases. To find changes in the cost function with respect to changes in a weight matrix , we need to introduce the idea of differentiating with respect to a matrix.
Exercise
Given , we define
where
Solution. We have
Therefore, the derivative with respect to
If
Example
Write two functions weight_gradients and bias_gradients which compute the derivatives with respect to
Solution. In each case, we calculate the derivative of the map to the next node (either
function weight_gradients(NN::NeuralNet,activations,gradients)
[gradients[purplenode(j)]' * activations[greennode(j)]' for j in 1:length(NN.maps)]
end
function bias_gradients(NN::NeuralNet,gradients)
[gradients[purplenode(j)]' for j in 1:length(NN.maps)]
end
@test weight_gradients(NN, activations, gradients) ==
[[-20 -30; 0 0], [70 0]]
@test bias_gradients(NN, gradients) == [[10, 0], [10]]Note that we have to transpose grads[purplenode(j)] since it is a row vector to begin with.
We are now set up to train the neural network.
Example
Write a function train which performs stochastic gradient descent: for a randomly chosen subset of the training set, determine the average desired change in weights and biases to reduce the cost function. Update the weights and biases accordingly and perform a specified number of iterations.
Your function should take 7 arguments: (1) desired architecture, (2) the activation function
Solution. We write a function which calculates the average suggested changes in the weights and biases and call it from inside the train function.
function suggested_param_changes(NN::NeuralNet, observations,
batch, ϵ)
arch = architecture(NN)
n_layers = length(arch)-1
sum_Δweight = [zeros(arch[i+1],arch[i]) for i in 1:n_layers]
sum_Δbias = [zeros(arch[i+1]) for i in 1:n_layers]
for k in batch
x, y = observations[k]
activations = forwardprop(NN,x)
gradients = backprop(NN,activations,y)
ΔWs = -ϵ*weight_gradients(NN,activations,gradients)
Δbs = -ϵ*bias_gradients(NN,gradients)
for i in 1:n_layers
sum_Δweight[i] += ΔWs[i]
sum_Δbias[i] += Δbs[i]
end
end
(sum_Δweight, sum_Δbias) ./ length(batch)
end Now we can write train. We initialize the biases to
function train(arch, K, K̇, observations, batchsize,
ϵ = 0.1, n_iterations = 1000)
random_maps = [AffineMap(randn(arch[i+1],arch[i]),
fill(0.1,arch[i+1])) for i in 1:length(arch)-1]
NN = NeuralNet(random_maps, K, K̇)
for i in 1:n_iterations
batch = sample(1:length(observations), batchsize)
meanΔweight, meanΔbias =
suggested_param_changes(NN, observations, batch, ϵ)
NN = NeuralNet(
[AffineMap(A.W + ΔW, A.b + Δb) for (A,ΔW,Δb) in
zip(NN.maps, meanΔweight, meanΔbias)], K, K̇
)
end
NN
end
Example
Try training your model on some data which are sampled by taking
Solution. We sample our data:
using Random; Random.seed!(123) xs = [rand(2) for i in 1:1000] ys = [[1-x'*x] for x in xs] observations = collect(zip(xs,ys))
Then we choose an architecture, a batch size, and a learning rate, and we train our model on the data:
arch = [2,5,1] batchsize = 100 ϵ = 0.005 NN = train(arch, K, K̇, observations, batchsize, ϵ, 10_000)
Finally, we inspect the result.
cost(NN::NeuralNet,observations) = mean(norm(NN(x)-y)^2 for (x,y) in observations) cost(NN,observations) # returns 0.00343 xgrid = 0:1/2^8:1 ygrid = 0:1/2^8:1 zs = [first(NN([x,y])) for x=xgrid,y=ygrid] using Plots; pyplot() surface(xgrid,ygrid,zs)
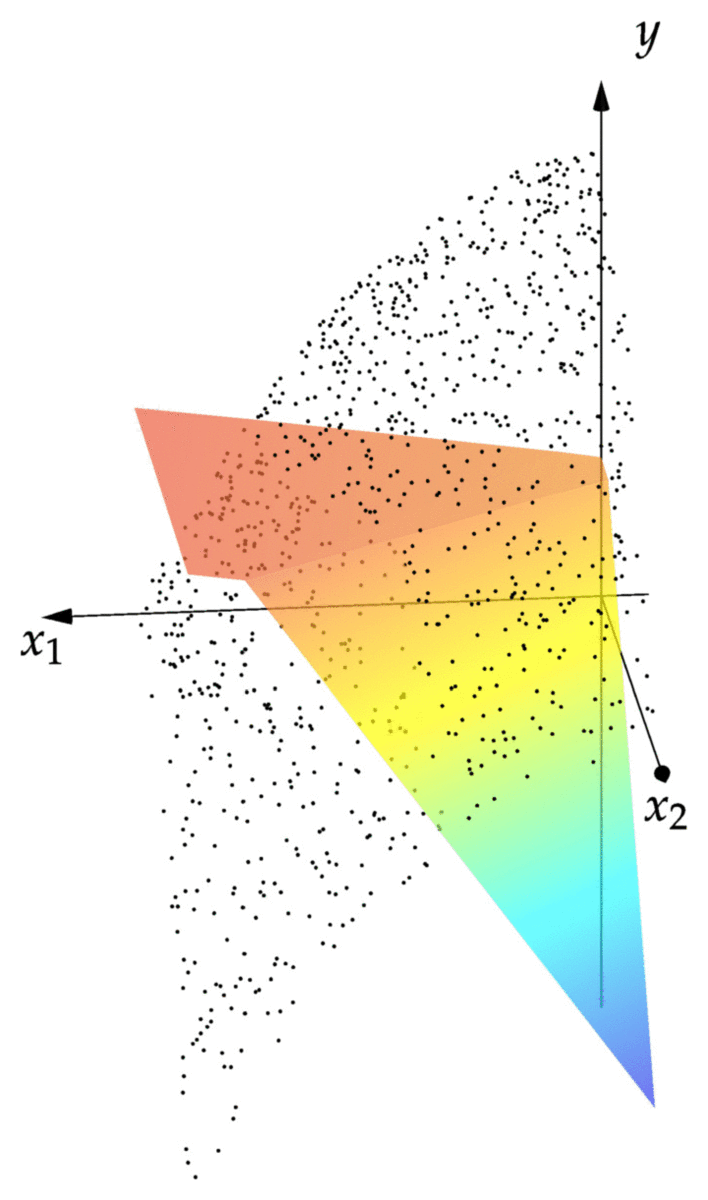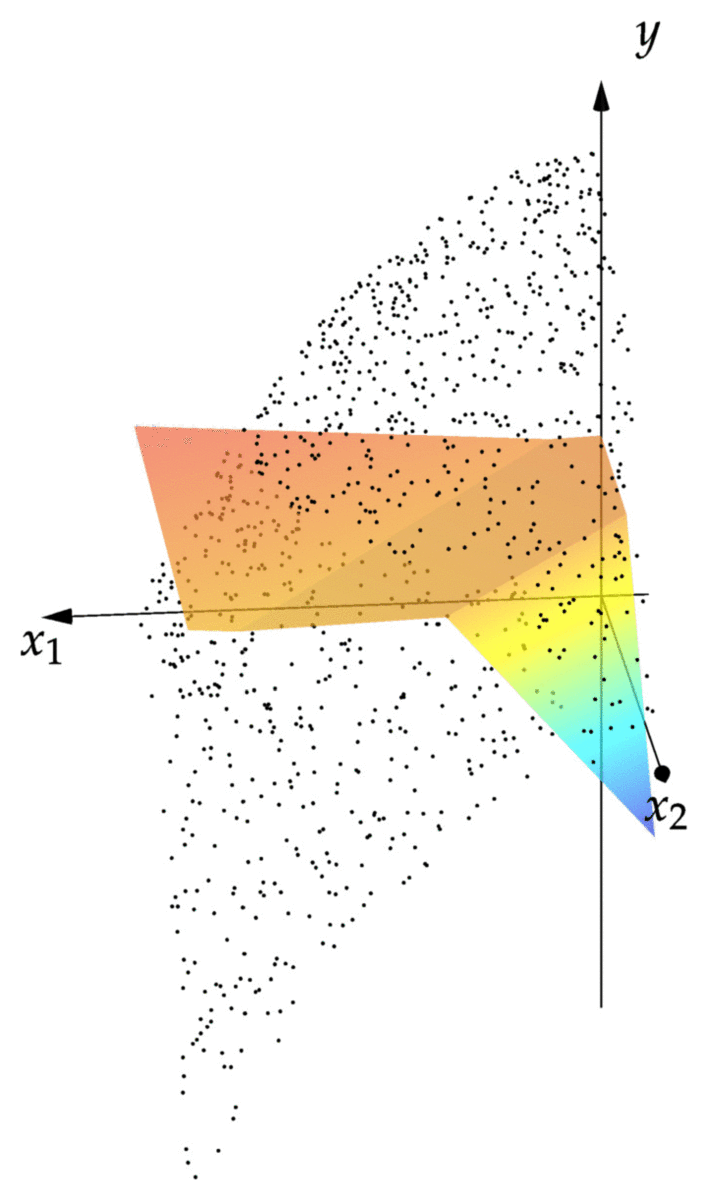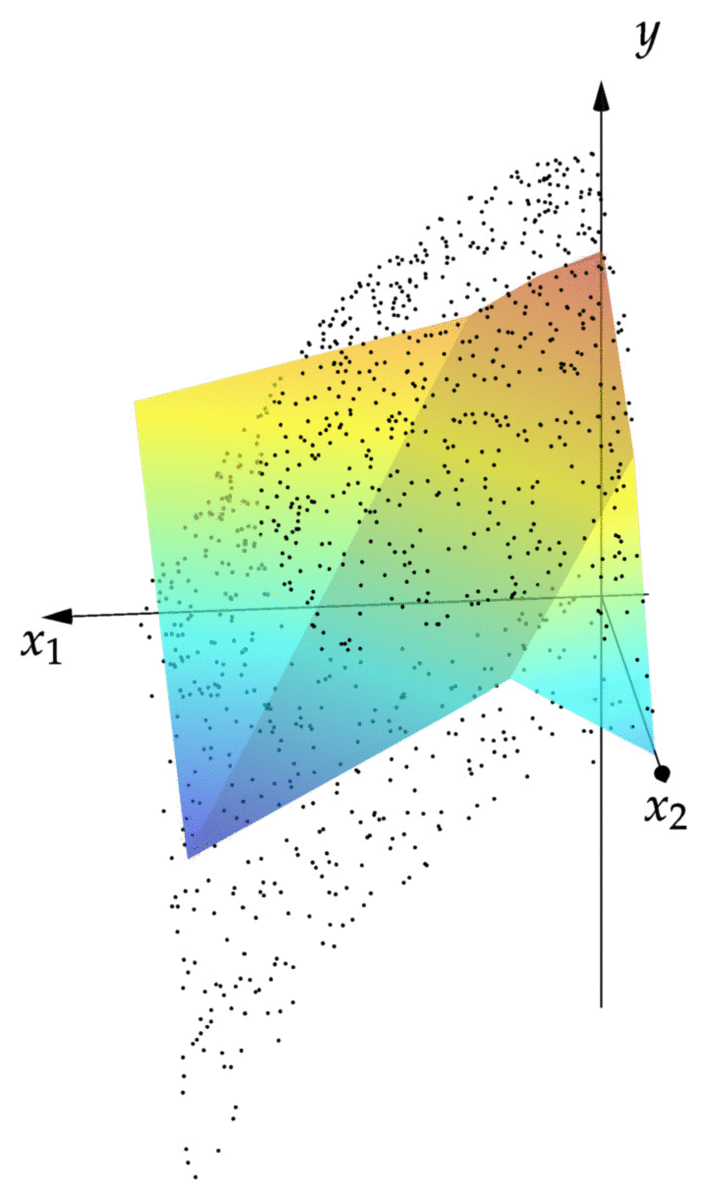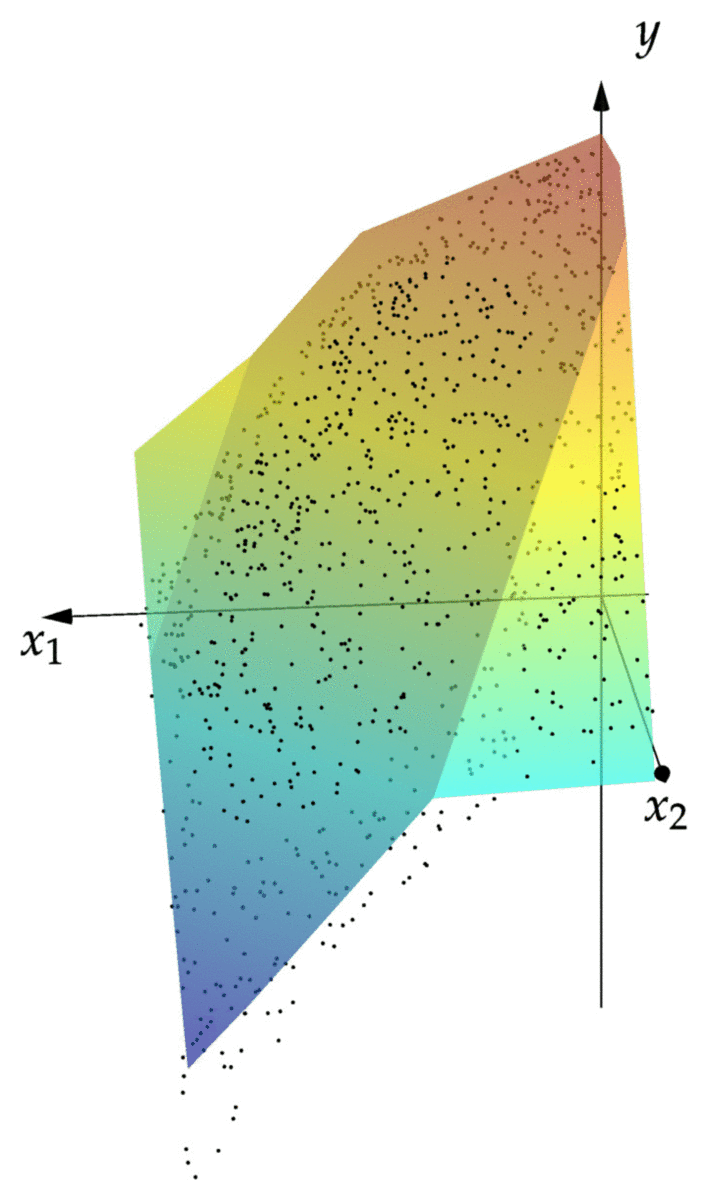
We can see that the resulting graph of