FractalesIntroducción
Al mirar alrededor de la naturaleza, es posible que haya notado plantas complejas como estas:


Este Helecho consiste en muchas hojas pequeñas que se ramifican de una más grande.


Este brócoli romanesco consiste en
Inicialmente, estos aparecen como formas muy complejas, pero cuando miras más de cerca, puedes notar que ambos siguen un patrón relativamente simple: todas las partes individuales de las plantas se ven exactamente igual que la totalidad planta, solo que más pequeña. El mismo patrón se repite una y otra vez, a escalas más pequeñas.
En matemáticas, llamamos a esta propiedad autosimilitud, y las formas que la tienen se llaman
Para crear nuestros propios fractales, tenemos que comenzar con un patrón simple y luego repetirlo una y otra vez, a escalas más pequeñas.
Uno de los patrones más simples podría ser un segmento de línea , con dos segmentos más que se ramifican desde un extremo. Si repetimos este patrón, ambos segmentos azules también tendrán dos ramas más en sus extremos.
Puede mover los puntos azules para cambiar la longitud y el ángulo de todas las ramas. Luego aumente el número de iteraciones usando
Dependiendo de la posición de las ramas, puedes hacer patrones completamente diferentes, como el arriba, un o . ¿Qué más puedes encontrar?
Otro famoso fractal es el
Observe cómo la forma final está compuesta de tres copias idénticas de sí misma, ¡y cada una de estas está compuesta de copias aún más pequeñas de todo el triángulo! Podrías seguir haciendo zoom en el triángulo para siempre, y los patrones y formas siempre continuarán repitiéndose.
Las plantas al comienzo de este capítulo se ven como fractales, pero es claramente imposible crear verdaderos fractales en la vida real. Si seguimos repitiendo el mismo patrón una y otra vez, cada vez más pequeños, eventualmente llegaríamos a células, moléculas o átomos que ya no se pueden dividir.
Sin embargo, usando las matemáticas, podemos pensar en las propiedades que los fractales reales "tendrían", y estas son muy sorprendentes ...
Dimensiones fractales
Primero, pensemos en la dimensión de los fractales. Una línea tiene dimensión
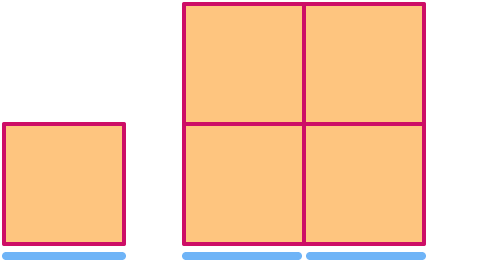
Un cuadrado tiene dimensión
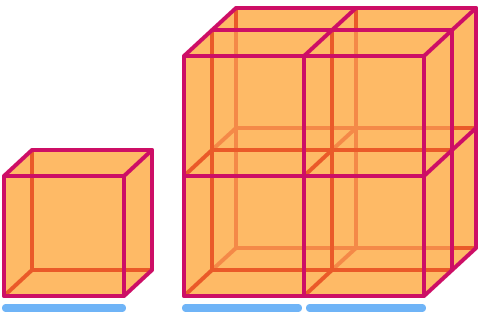
Un cubo tiene dimensión
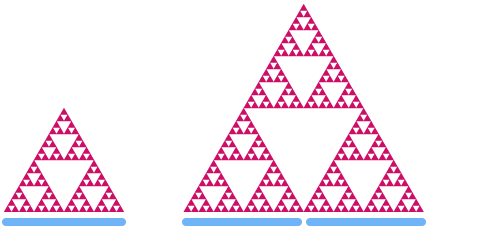
Ahora echemos un vistazo al triángulo de Sierpinski. Si lo escalamos por un factor de 2, puede ver que su "área" aumenta en un factor de
Digamos que d es la dimensión del triángulo de Sierpinski. Usando el mismo patrón que el anterior, obtenemos
Pero espera ... ¿cómo puede algo tener una dimensión que no sea un número entero? Parece imposible, pero esta es solo una de las propiedades extrañas de los fractales. De hecho, esto es lo que les da su nombre a los fractales: tienen una dimensión fraccional.
Con cada iteración, eliminamos parte del área del triángulo de Sierpinski. Si pudiéramos hacer esto infinitamente muchas veces, en realidad no quedaría ningún área: es por eso que el triángulo de Sierpinski es algo entre un área bidimensional y una línea unidimensional.
Mientras que muchos fractales son auto-similares, una mejor definición es que fractales son formas que tienen una dimensión no entera.
El copo de nieve de Koch
Hay muchas formas en la naturaleza que parecen fractales. Ya hemos visto algunas plantas al comienzo de este capítulo. Otros grandes ejemplos son los copos de nieve y los cristales de hielo:
Para crear nuestro propio copo de nieve fractal, una vez más tenemos que encontrar un procedimiento simple que podamos aplicar una y otra vez.
Al igual que el triángulo de Sierpinski, comencemos con un solo triángulo equilátero. Sin embargo, en lugar de eliminar triángulos más pequeños en cada paso, agregamos triángulos más pequeños a lo largo del borde. La longitud lateral de cada triángulo es
La forma resultante se llama
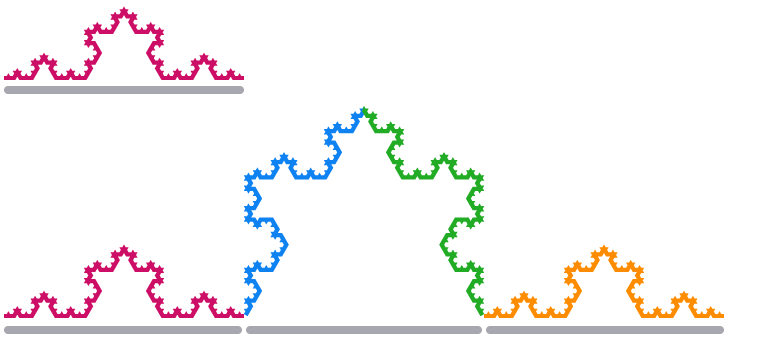
Cuando escalamos un segmento de borde del Copo de nieve Koch por un factor de 3, su longitud
Usando la misma relación entre dimensiones y factores de escala que el anterior, obtenemos la ecuación
Área
Crear los copos de nieve Koch es casi como una secuencia




Después de la primera iteración, el número de nuevos triángulos agregados aumenta en un factor de
Digamos que el
Usando la fórmula para la suma de infinitas
Perímetro
También podemos intentar calcular el perímetro del copo de nieve de Koch. Como ya hemos visto antes, la longitud del perímetro cambia por un factor de
Esto significa que, una vez más, tenemos una serie geométrica, pero en este caso,

Si esto parece contradictorio, solo recuerda que multiplicamos el perímetro por
Es casi impensable que pueda tener una forma con un área finita y también una circunferencia infinita, pero esta es solo una de las muchas propiedades inesperadas de los fractales.
¿Puedes encontrar alguna otra forma de crear tus propios fractales?
"Mi alma está en espiral en fractales congelados por todas partes ..."
esponja Menger
Los fractales no tienen que ser "planos", como muchos de los ejemplos anteriores. Uno de los fractales más famosos que parecen tridimensionales es la esponja Menger, llamada así por el matemático
Comenzamos con un cubo sólido, y repetidamente taladramos agujeros cada vez más pequeños en sus lados. Cada nueva iteración de agujeros tiene
Un cubo
Ahora podemos intentar calcular la dimensión d de la esponja Menger tal como lo hicimos para el copo de nieve de Koch arriba. En este caso obtenemos
Si imagina cortar más y más agujeros, infinitas veces, no quedaría ningún volumen real. ¡Es por eso que el cubo es "no del todo" tridimensional!
Costas fractales
Una de las características clave de todos los fractales que hemos visto hasta ahora es que puedes "acercar" para siempre y siempre encontrar nuevos patrones. Alrededor de 1920, el matemático británico
Comienza con la forma básica del país y, a medida que se acerca, agrega entradas de ríos, bahías y estuarios, luego acantilados individuales, rocas, guijarros, etc.
Este es un problema importante cuando se trata de calcular la longitud de la frontera de un país: ¿cómo decide hasta qué punto acercarse y qué rincones y grietas incluir?
Una manera de medir la longitud de la costa de Gran Bretaña, por ejemplo, es tomar una regla larga, caminar alrededor de sus playas y luego sumar todas las distancias.
Si la regla tiene
Podemos seguir adelante, con gobernantes cada vez más pequeños, y cada vez que nuestro resultado para la longitud de la costa sea un poco más largo. Al igual que el Copo de nieve de Koch, ¡parece que la costa de Gran Bretaña es infinitamente larga! Esto a menudo se llama la paradoja de la costa.
Algunas décadas más tarde, el matemático
La costa de Gran Bretaña ciertamente "parece" fractal, pero no es auto-similar, como otros fractales que hemos visto antes. Para encontrar su tamaño, podemos dibujarlo en una cuadrícula y contar el número de celdas con las que se cruza.
Inicialmente, hay 88 celdas de intersección. Si escalamos la costa por un factor de 2, hay 197 celdas que se cruzan, ¡más del doble!
El tamaño de la costa ha aumentado en un factor de
Si repetimos esto con cuadrículas más grandes, encontraremos que la dimensión de la costa de Gran Bretaña es en realidad aproximadamente 1.21. Mandelbrot se dio cuenta de que esta dimensión fractal también es una medida de la rugosidad de una forma, un nuevo concepto, para el cual encontró importantes aplicaciones en muchas otras áreas de las matemáticas y las ciencias.
Más fractales en la naturaleza y la tecnología
Si bien los verdaderos fractales nunca pueden aparecer en la naturaleza, hay muchos objetos que se parecen casi a fractales. Ya hemos visto plantas, copos de nieve y costas, y aquí hay algunos ejemplos más:
Cordillera en Asia central
Delta del río Ganges en India
Rayos
Vasos sanguíneos en la retina
Gran Cañón en los EE. UU.
Nubes
Todos estos objetos pueden aparecer completamente al azar, pero, al igual que los fractales, hay un patrón subyacente que determina cómo se forman. Las matemáticas pueden ayudarnos a comprender mejor las formas, y los fractales tienen aplicaciones en campos como la medicina, la biología, la geología y la meteorología.
Terreno fractal generado por computadora
También podemos usar fractales para crear "copias" realistas de la naturaleza, por ejemplo, como paisajes y texturas utilizadas en videojuegos o películas generadas por computadora. ¡El agua, las montañas y las nubes en esta imagen están hechas completamente por una computadora, con la ayuda de fractales!
E incluso podemos revertir este proceso para comprimir imágenes digitales, para reducir su tamaño de archivo. Los primeros algoritmos fueron desarrollados por Michael Barnsley y Alan Sloan en la década de 1980, y todavía se están investigando nuevos.