FractalesEl conjunto de Mandelbrot

Todos los fractales que vimos en los capítulos anteriores se crearon utilizando un proceso de iteración: comienzas con un patrón específico y luego lo repites una y otra vez.

Esto es similar a otro concepto en matemáticas que viste antes: con secuencias recursivas, comienzas con un número específico, y luego aplicas la misma fórmula recursiva, una y otra vez, para obtener el siguiente número en el secuencia.

Tomemos como ejemplo la fórmula recursiva xn=xn−12 y grafiquemos sus términos en una recta numérica. Puede cambiar el valor de x0:

Observe cómo la secuencia resultante puede comportarse de manera muy diferente, dependiendo del valor inicial x0:

Hasta ahora, no hemos aprendido nada nuevo. Sin embargo, hace aproximadamente un siglo, los matemáticos comenzaron a explorar qué sucede con estas secuencias si usas números complejos, en lugar de solo la recta numérica real. Sus descubrimientos fueron algunos de los resultados más sorprendentes y hermosos en todas las matemáticas.

Conjuntos de Julia

Usemos la misma secuencia que antes, xn=xn−12, pero en el plano complejo. Puede mover la posición de x0 para ver qué sucede con los siguientes términos. Si parece que la secuencia convergerá, coloreemos el punto correspondiente en el plano en azul:

Como puede ver, la secuencia converge siempre que x0 se encuentre dentro del círculo unitario outside the unit squareabove the >>>>x<<<<-axis (el círculo con radio 1, centrado en el origen).

Ahora hagamos las cosas un poco más difíciles. En lugar de simplemente cuadrar el número anterior, también agregamos una constante c cada vez (que puede ser cualquier número complejo). En otras palabras, xn=xn−12+c. ¿Crees que todavía obtendremos un círculo de convergencia? ¿Qué otras formas crees que podríamos ver? Continuar

En este diagrama, puede mover la posición de x0 así como el valor de c:

Las diferentes formas que se forman coloreando los números se llaman Conjuntos de Julia. Fueron descubiertos independientemente por dos matemáticos franceses, Gaston Julia y Pierre Fatou, alrededor de 1918.

En ese momento, no había computadoras para ayudar a visualizar cómo se veían los conjuntos de Julia. Los matemáticos como Julia y Fatou pudieron razonar matemáticamente sobre ellos, pero solo vieron bocetos a mano y toscos de cómo se verían.

Hoy no tenemos este problema: las imágenes a continuación son todos conjuntos de Julia diferentes. Los diferentes colores indican qué tan rápido la secuencia en ese punto diverge:

Continuar

El conjunto de Mandelbrot

Al crear los diferentes conjuntos de Julia, es posible que haya notado que había algunos valores de c para los cuales cada secuencia diverge, y todo el plano complejo permanece blanco. Unas pocas décadas después de Julia y Fatou, una nueva generación de matemáticos intentó mapear cómo se veían estas áreas.

En el ejemplo anterior, elegimos un valor fijo para c, y luego cambiamos la posición de x0 para colorear el plano. Ahora arreglemos el valor de x0=0 y, en su lugar, cambiemos el valor de c.

Una vez más, pinta sobre el plano complejo para revelar el área en la que las secuencias permanecen delimitadas. ¿Qué formas esperas que aparezcan?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Este fractal se llama Conjunto de Mandelbrot, y cuando se gira 90 °, se ve casi como una persona, con cabeza, cuerpo y dos brazos. Fue definido y dibujado por primera vez en 1978, en un trabajo de investigación de los matemáticos Robert Brooks y Peter Matelski:

Unos años más tarde, Benoit Mandelbrot utilizó las potentes computadoras de IBM para crear una visualización mucho más detallada del fractal, que más tarde recibió su nombre. Las primeras impresiones se veían diferentes de lo que esperaba, hasta que se dio cuenta de que los técnicos que trabajaban en las impresoras estaban limpiando la "borrosidad" alrededor de su borde, suponiendo que fue causada por partículas de polvo o errores de la impresora, y no una característica definitoria de los fractales. ! Continuar

Como todos los fractales, podemos "acercarnos" al conjunto de Mandelbrot para siempre, encontrando nuevos patrones en cada escala. Aquí puede ampliar una parte del conjunto de Mandelbrot que se llama Seahorse valley. Los puntos negros son dentro de el conjunto de Mandelbrot, donde la secuencia está limitada. Los puntos de color están fuera de del conjunto de Mandelbrot, donde la secuencia diverge, y los diferentes colores indican qué tan rápido crece hasta el infinito:

Scale: ${pow(scale)}

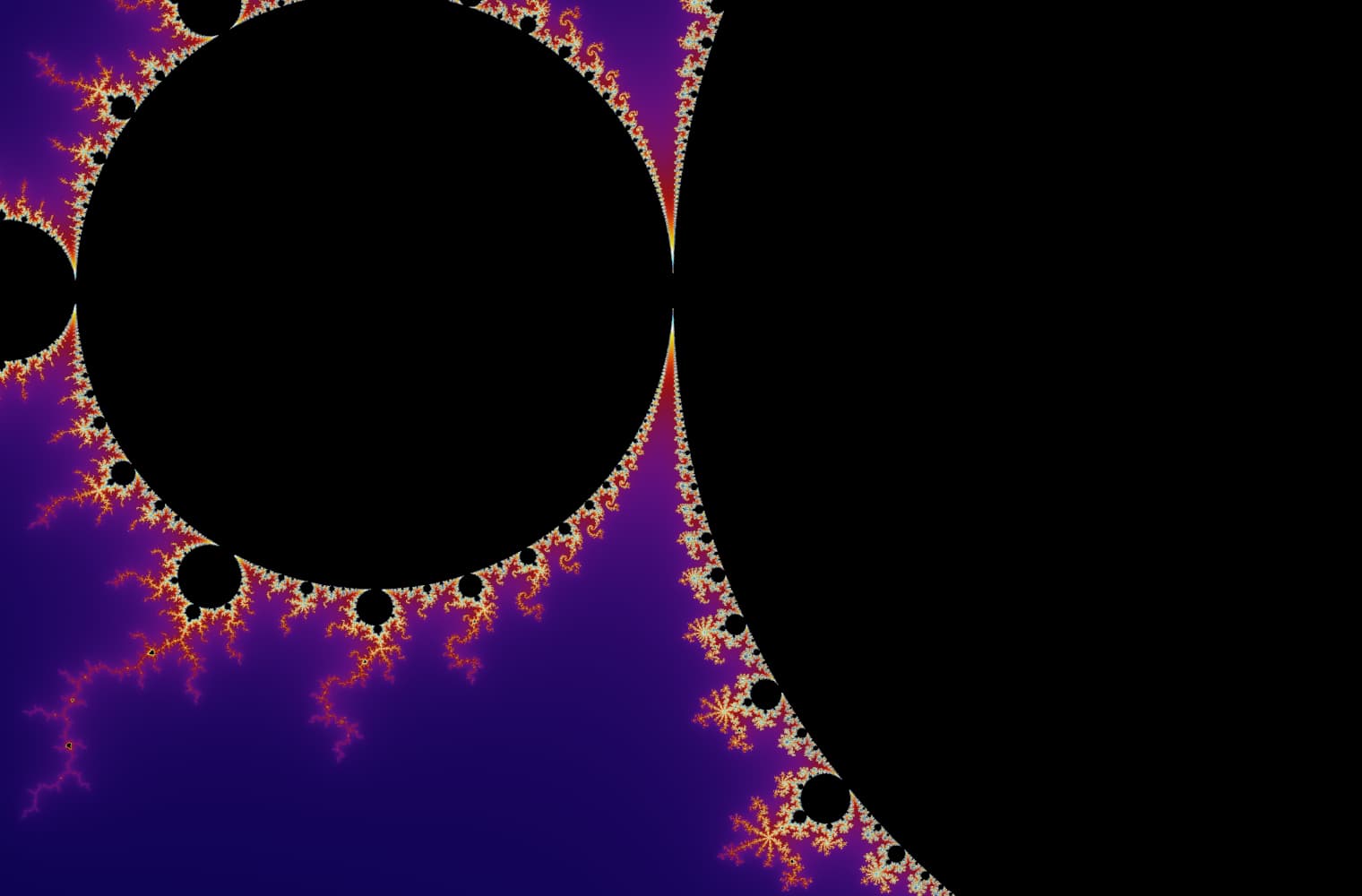
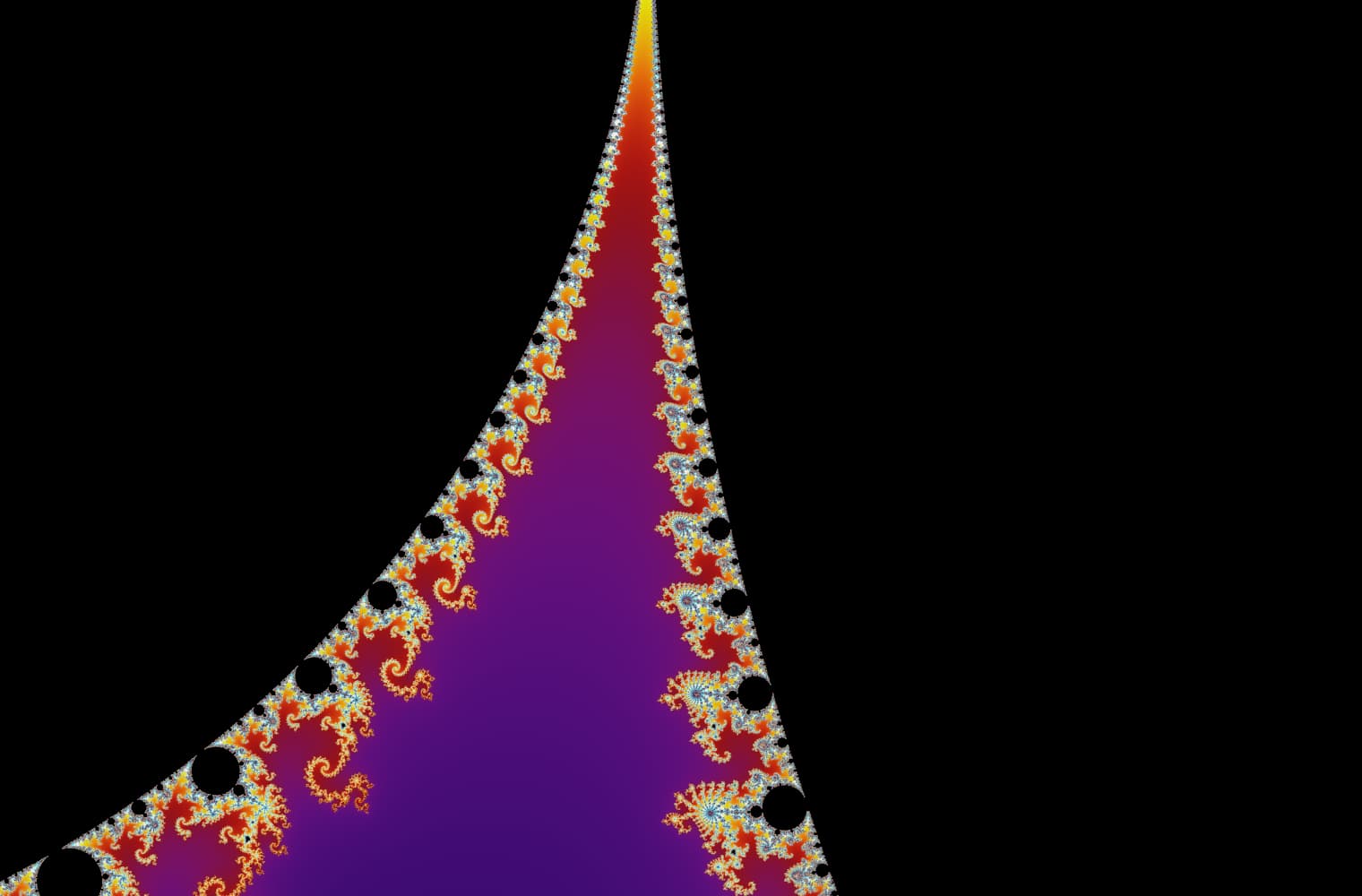
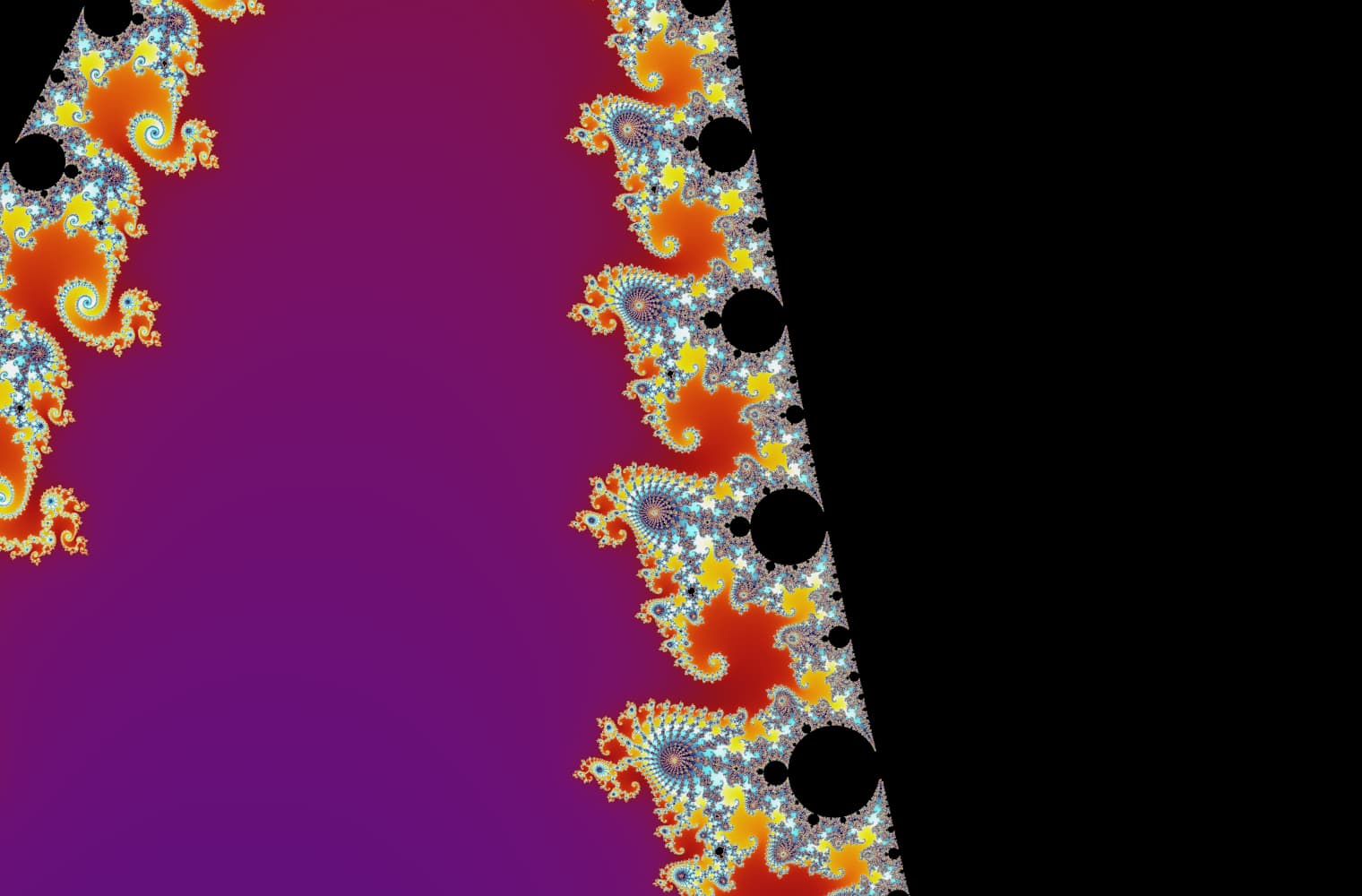
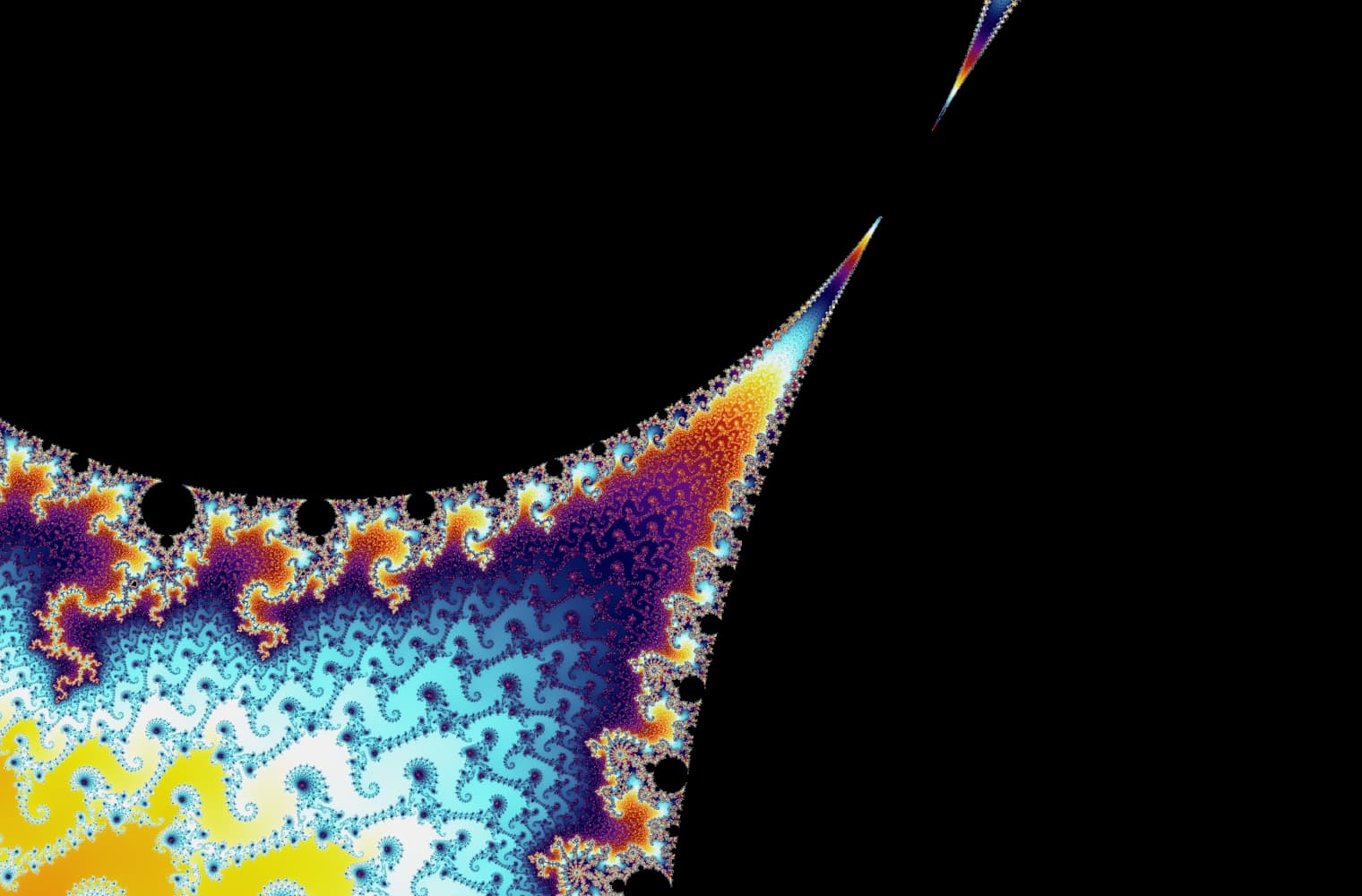
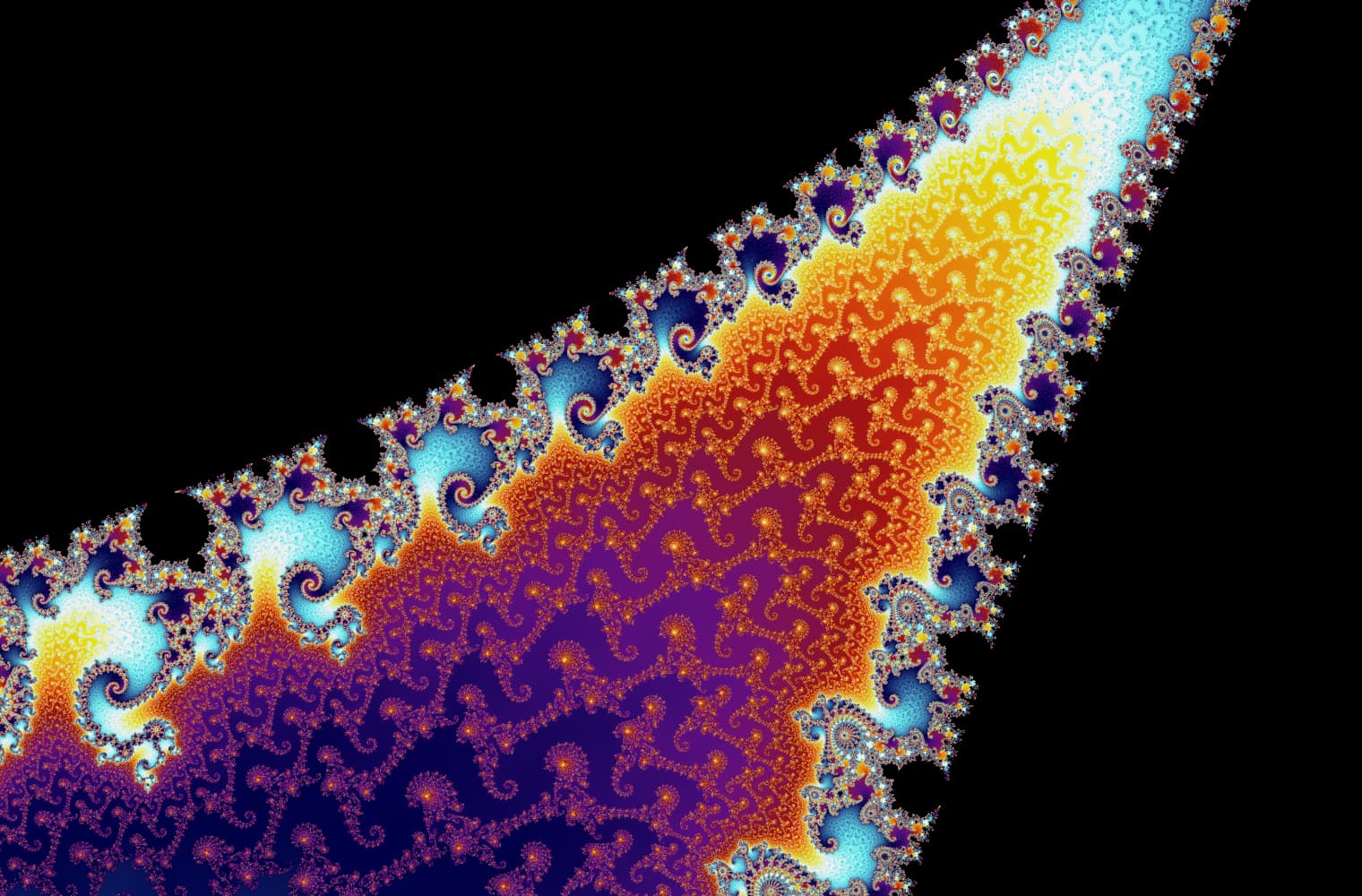
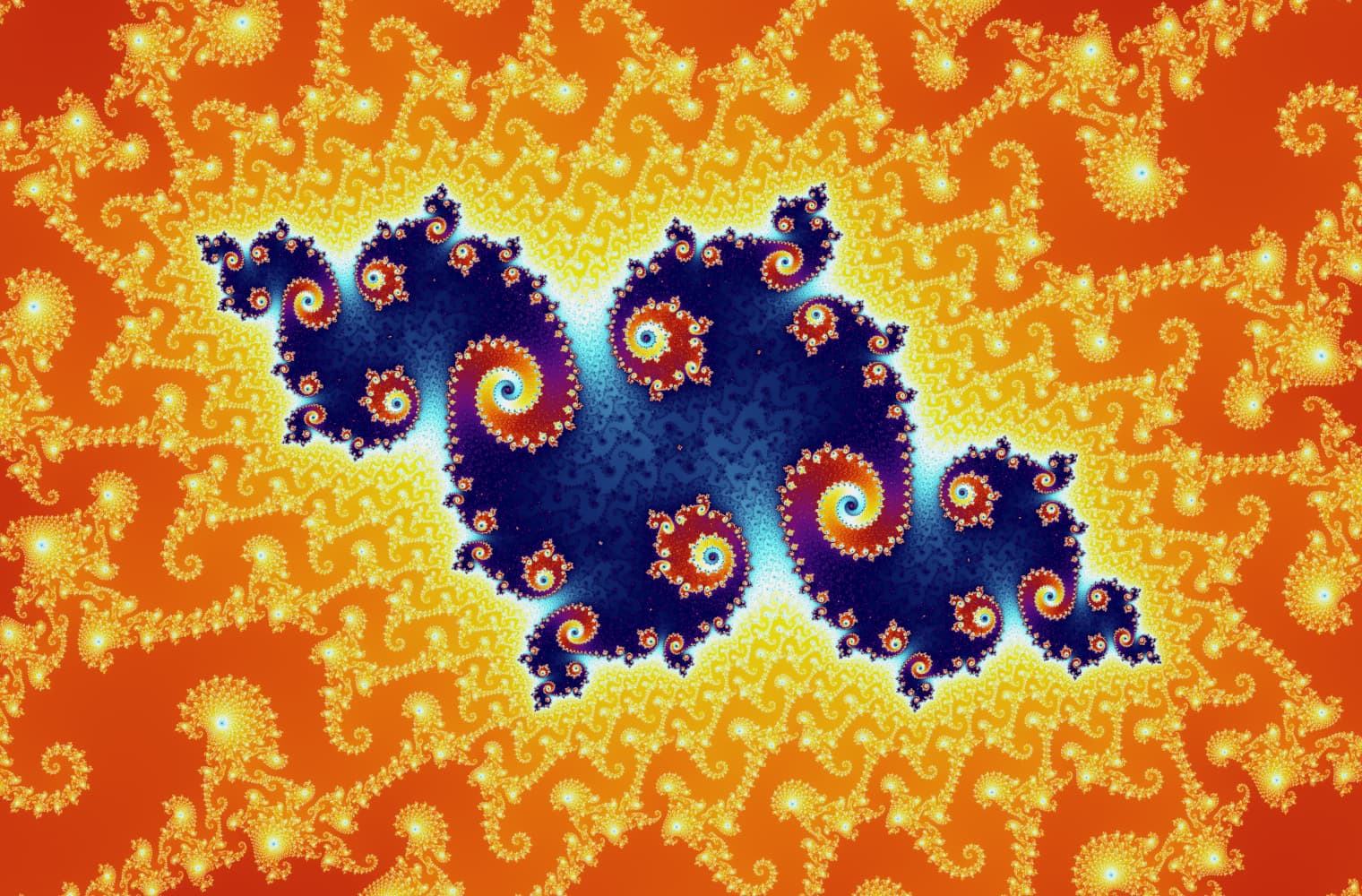
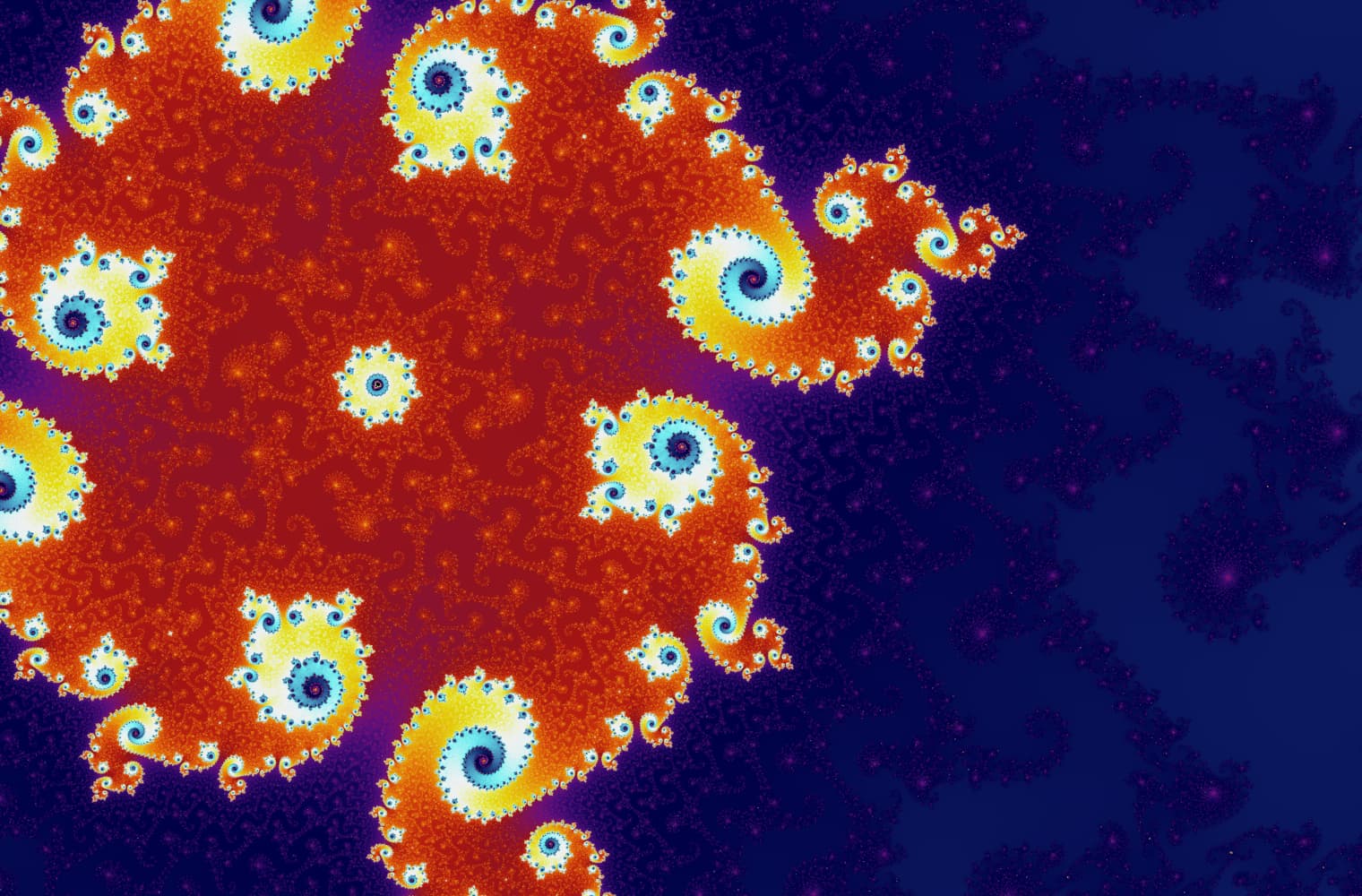
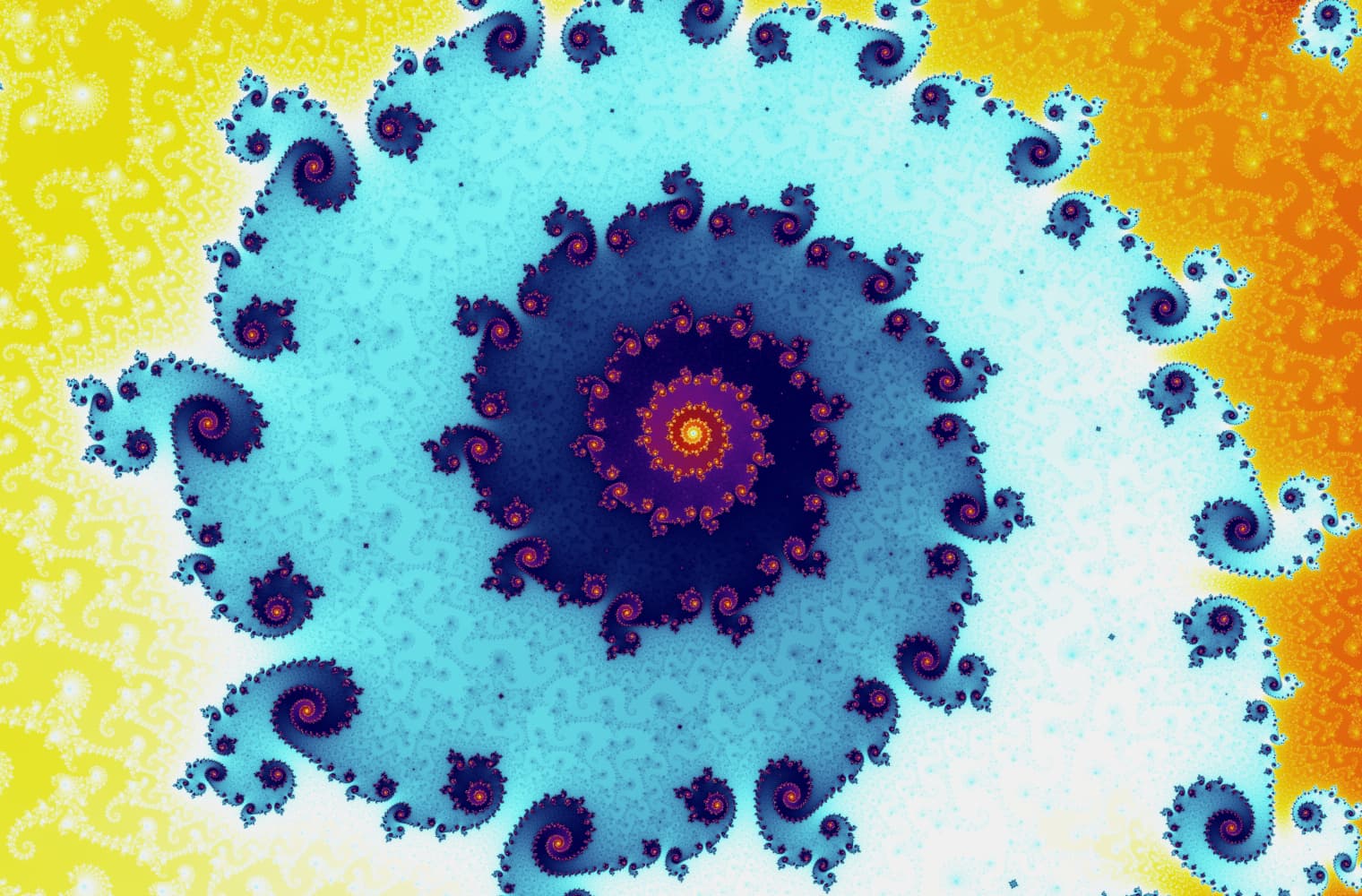
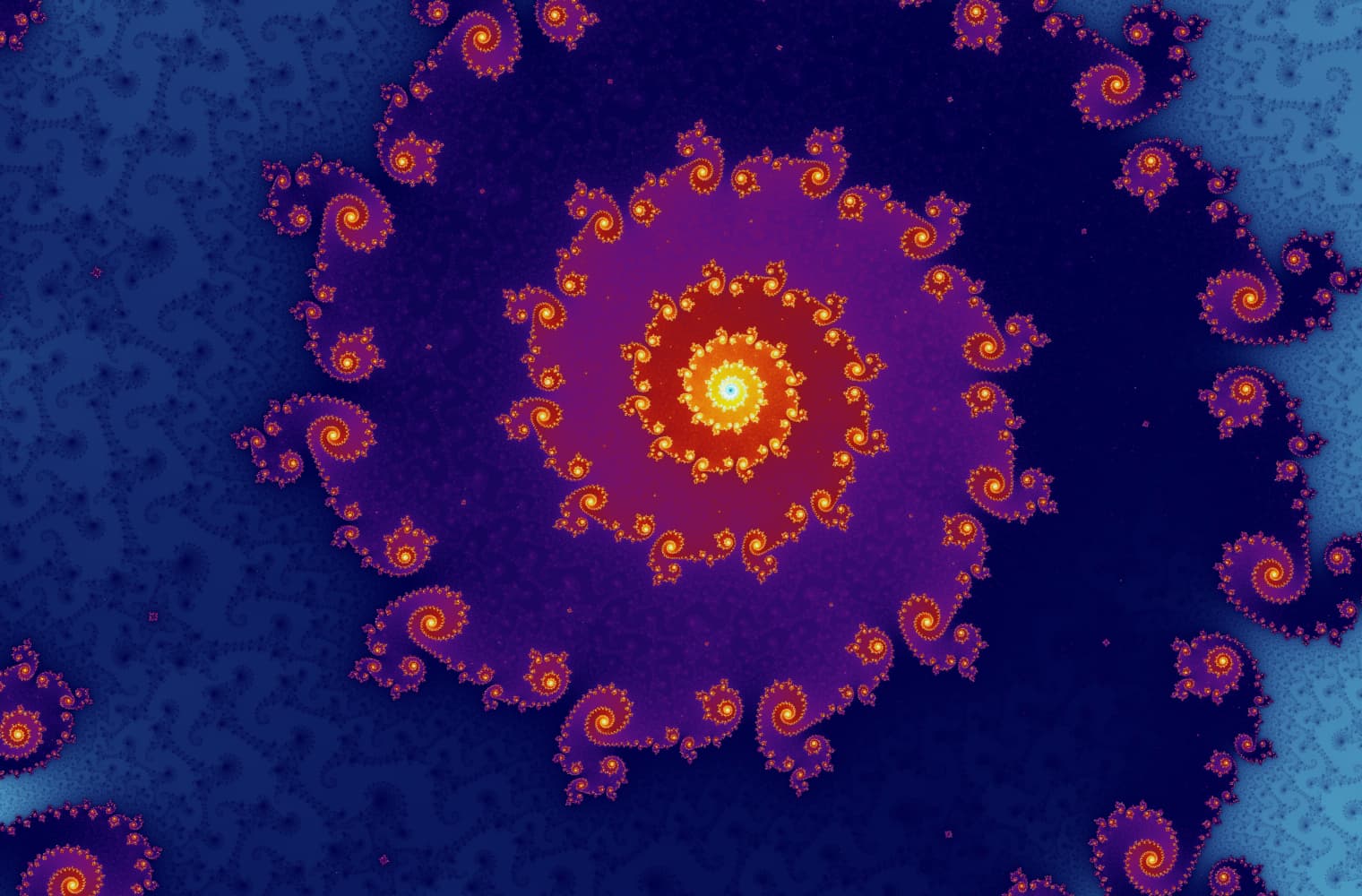
Este control deslizante consta de 27 imágenes individuales, hasta un nivel de zoom de más de 14 billones, o 254. En total, tomaron casi 45 minutos para renderizar en una computadora portátil moderna. El conjunto de Mandelbrot se puede crear con una sola ecuación simple, xn=xn−12+c, pero es infinitamente complejo e increíblemente hermoso.

A medida que mueve el valor de c alrededor del conjunto de Mandelbrot, puede notar una propiedad curiosa:

• Todas las secuencias dentro del cuerpo principal del conjunto Mandelbrot convergendivergereach an orbit en un solo punto.
• Las secuencias dentro del bulbo grande en la parte superior alcanzan una órbitaconvergediverge que consta de puntos.
• Las secuencias en esta bombilla más pequeña tienen órbitas de longitud .

Cada bombilla tiene una órbita de diferente tamaño, con bombillas más pequeñas que tienen más y más puntos en sus órbitas. El tamaño de estas órbitas está estrechamente relacionado con el Mapa logístico, un concepto importante en Teoría del caos.