Rompecabezas de rompecabezas

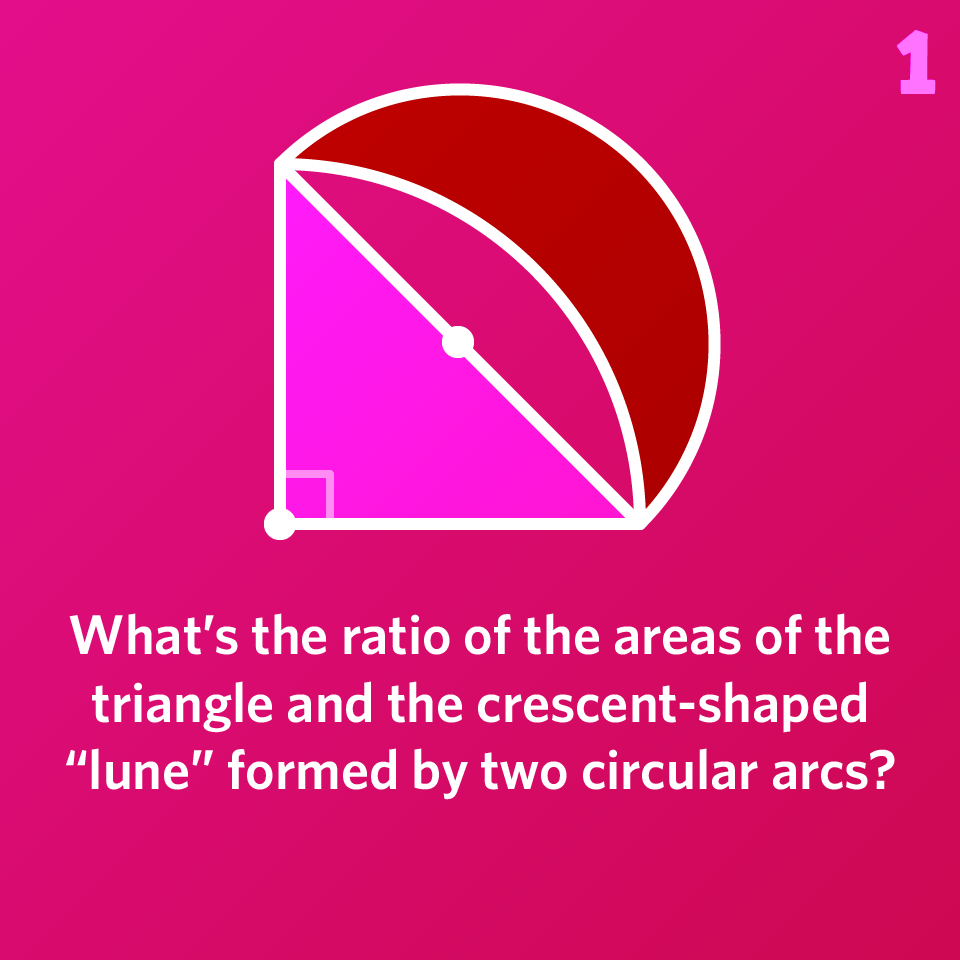
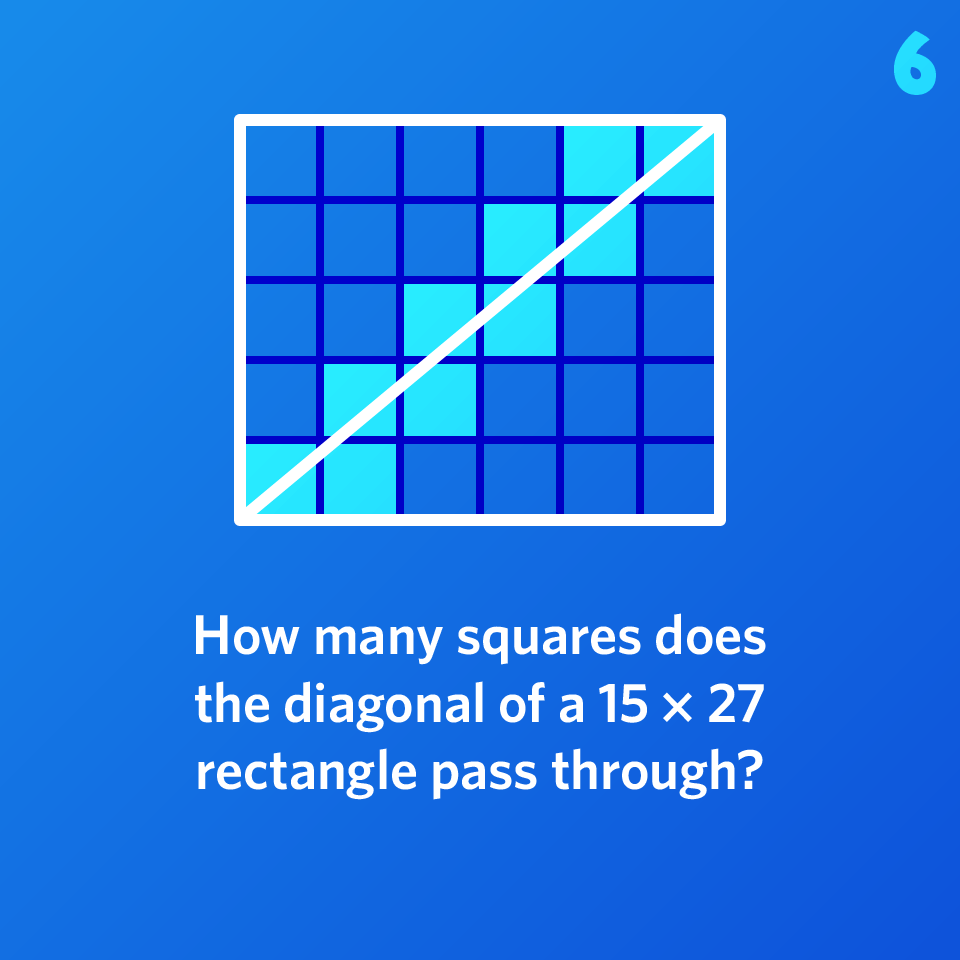
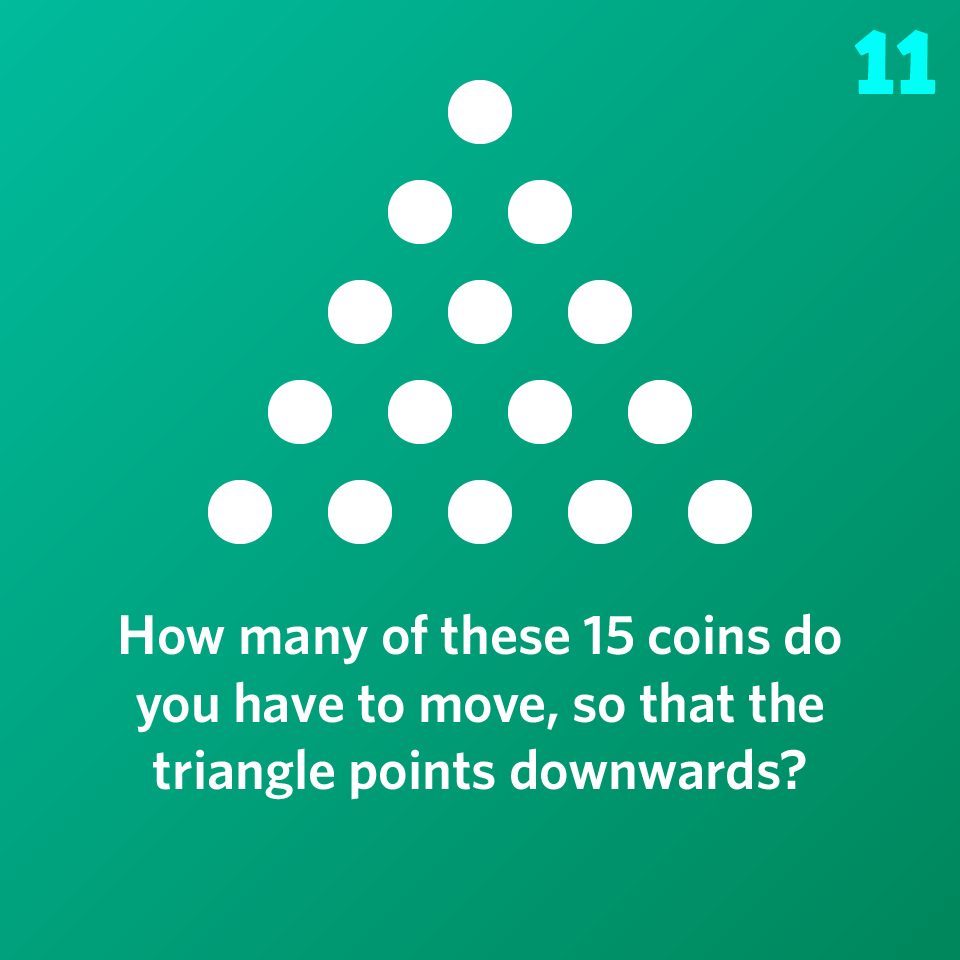
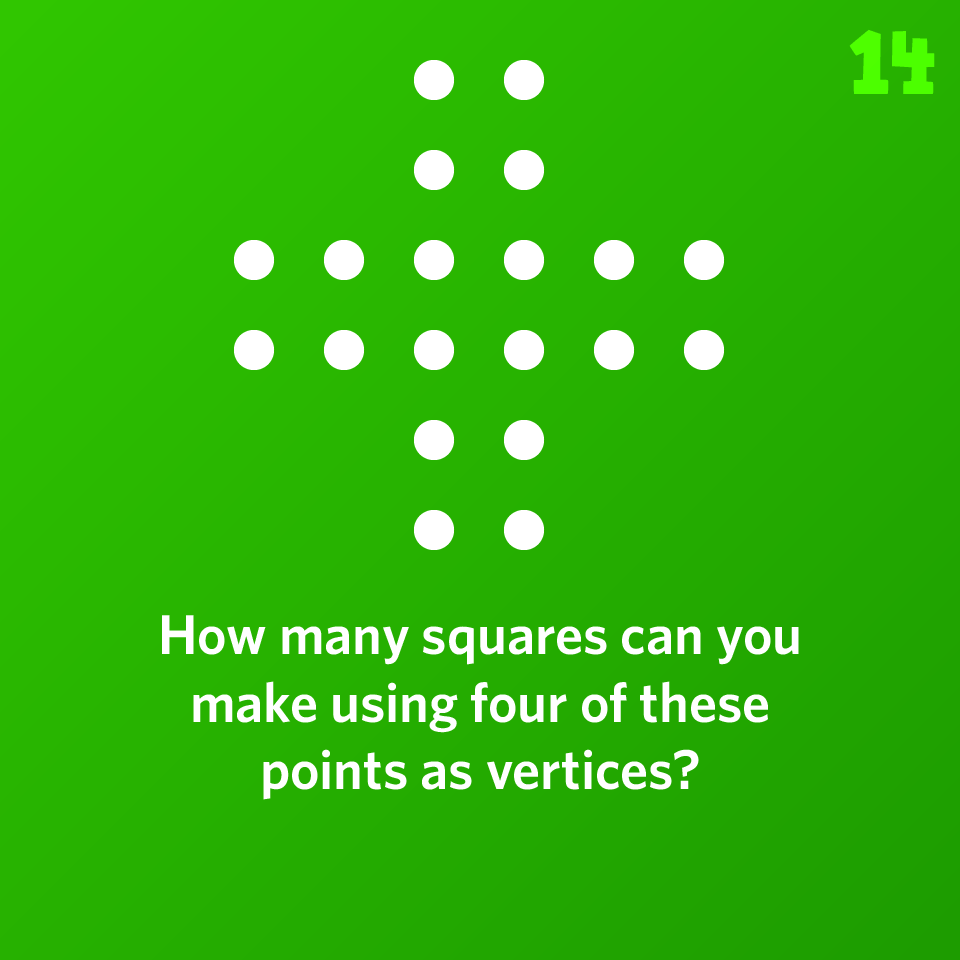
What’s the ratio of the areas of the triangle and the crescent-shaped “lune” formed by two circular arcs?

Please sign in to see the solution.

How many non-attacking knights can be placed on a chessboard?

Please sign in to see the solution.

A deck of 52 cards is shuffled. On average, how many cards do you expect to remain in exactly the same position as before the shuffle?

Please sign in to see the solution.

What is the area of the shape enclosed by these six hat mono-tiles?

Please sign in to see the solution.

What’s the next number in this sequence?

1, 3, 4, 7, 11, 18, ?, ?

Please sign in to see the solution.

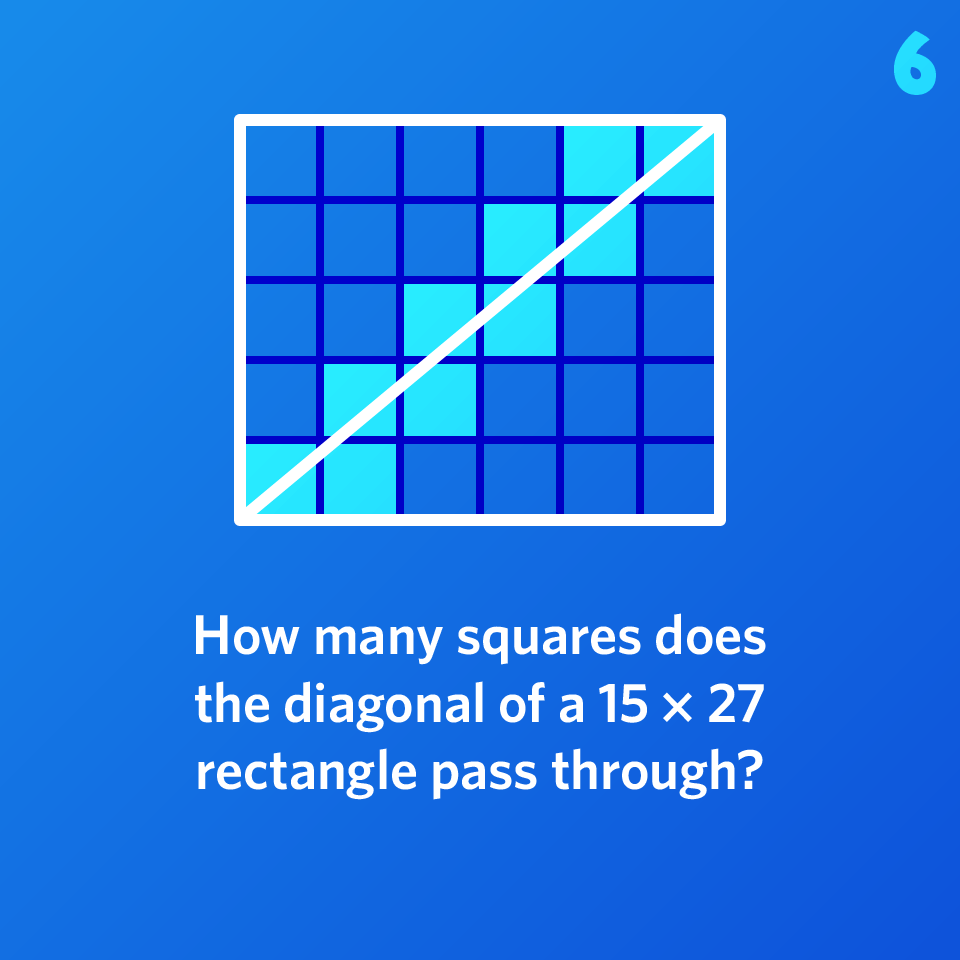
How many squares does the diagonal of a 15 × 27 rectangle pass through?

Please sign in to see the solution.

Here is a 3 × 4 grid of stamps. How many different ways are there to tear off four stamps (still joined together along their sides)?

Please sign in to see the solution.

What proportion of this bottle is filled with water?

Please sign in to see the solution.

Can you cut this right-angled triangle with smaller sides 1 and 2 into five identical triangles, each similar to the big triangle?

Please sign in to see the solution.

How many numbers between 1 and 9999 consist of at most two different digits?

Please sign in to see the solution.

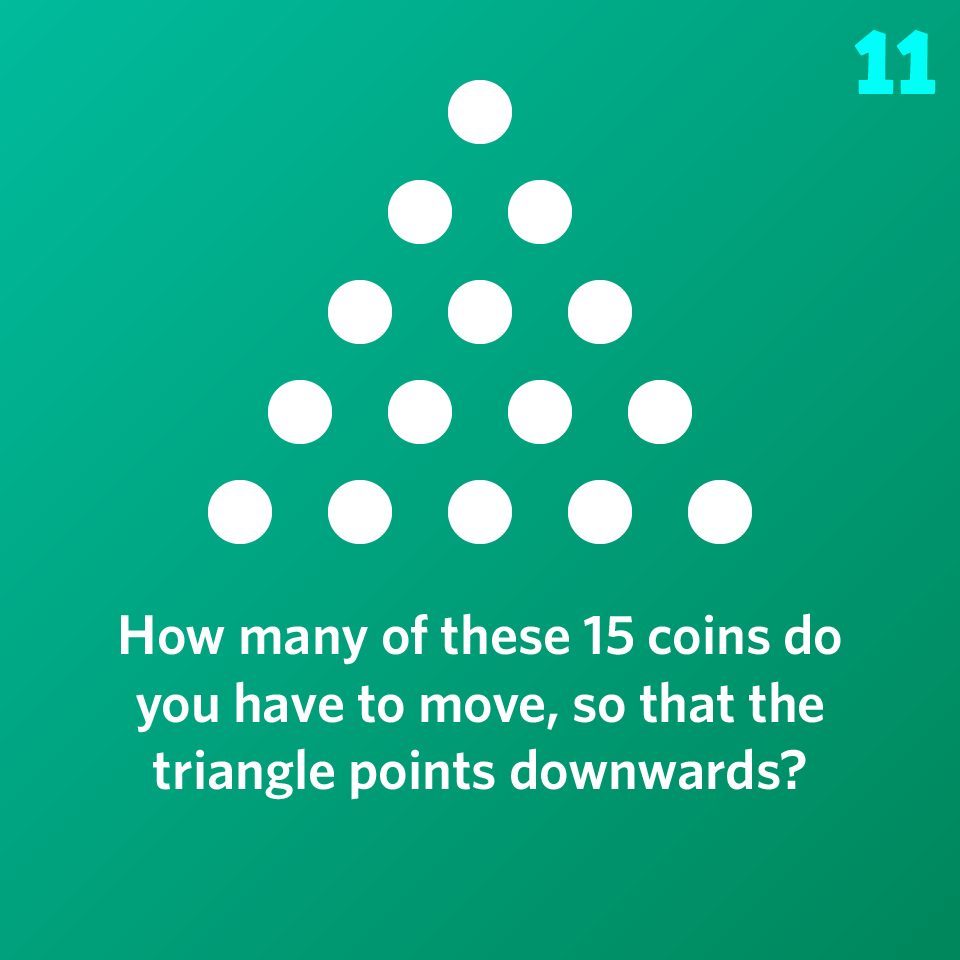
How many of these 15 coins arranged in a triangle do you have to move, so that the triangle points downwards?

Please sign in to see the solution.

One cut divides a cake into 2 pieces.
Two cuts can divide it into 4 pieces.
Three cuts can divide it into 7 pieces.

What is the maximum number of pieces you can make with 10 cuts?

Please sign in to see the solution.

Five people A, B, C, D and E are seated randomly around a round table. What is the probability that A and B are next to each other?

Please sign in to see the solution.

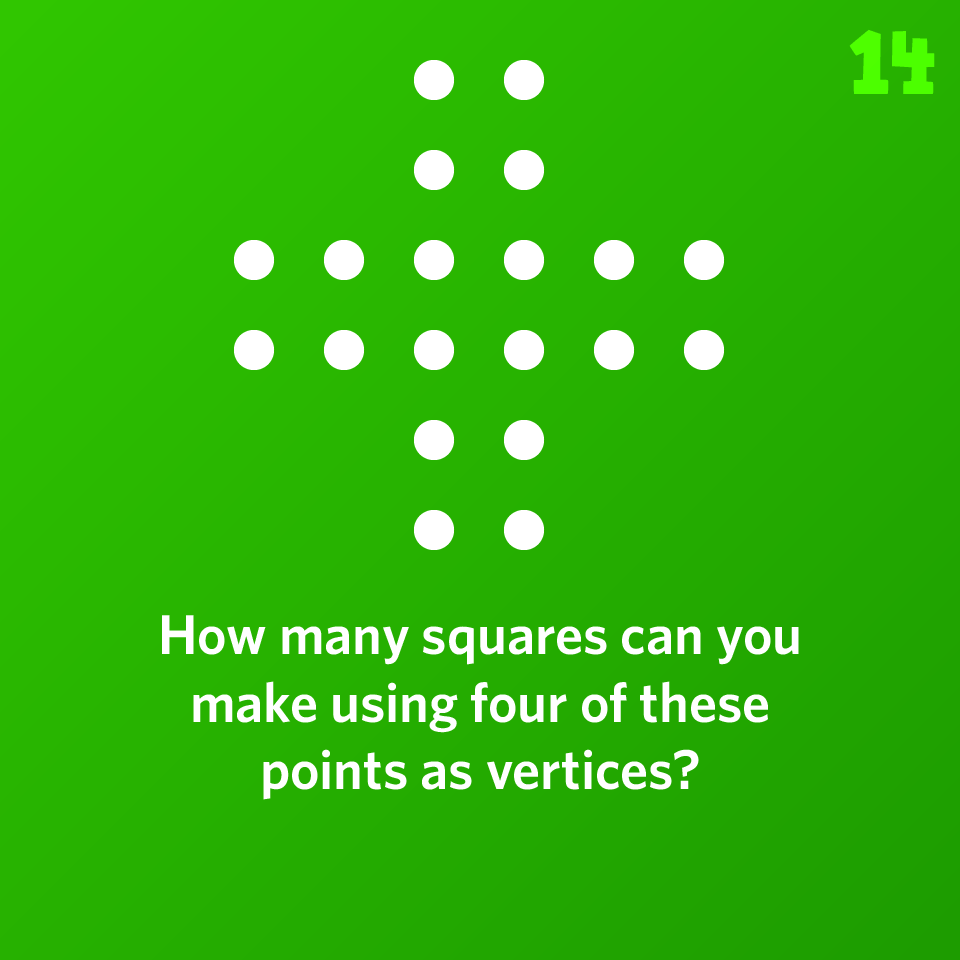
How many squares can you make using four of these points as vertices?

Please sign in to see the solution.

Rearrange these 8 prime numbers and 1 into a magic square where every row and column adds up to the same number.

Please sign in to see the solution.

A semicircle is placed inside a square of size 1. What is the diameter d of the semicircle?

Please sign in to see the solution.

You and your friend both throw a fair die. What is the probability that you get a higher number?

Please sign in to see the solution.

How many different necklaces can be made using five identical blue beads, and two identical yellow beads?

Please sign in to see the solution.

Use a single, straight-line to cut this shape into two pieces that can be rearranged into a square.

Please sign in to see the solution.

What is the sum of all the digits of the numbers from 1 to 100?

1 + 2 + 3 + … + (9 + 9) + (1 + 0 + 0)

Please sign in to see the solution.

Can you make all these shapes using the seven Tangram pieces?

Please sign in to see the solution.

What’s the probability that the ball will land in bucket B?

Please sign in to see the solution.

All three circles have radius 1. What is the radius of the larger semicircle?

Please sign in to see the solution.

What is the least number of moves needed to transfer all seven disks from the first tower to the last, without placing a larger disk on a smaller one?

Please sign in to see the solution.

Can you cut each of these two shapes into four identical pieces?

Please sign in to see the solution.

What six digits should be placed on the second die, so that the distribution of the sum of both dice is the same as two normal dice?

The first die contains faces numbered 1, 2, 2, 3, 3, 4.

Please sign in to see the solution.

Place the digits from 1 to 7 into each of these regions, so that every circle has the same sum.

Please sign in to see the solution.

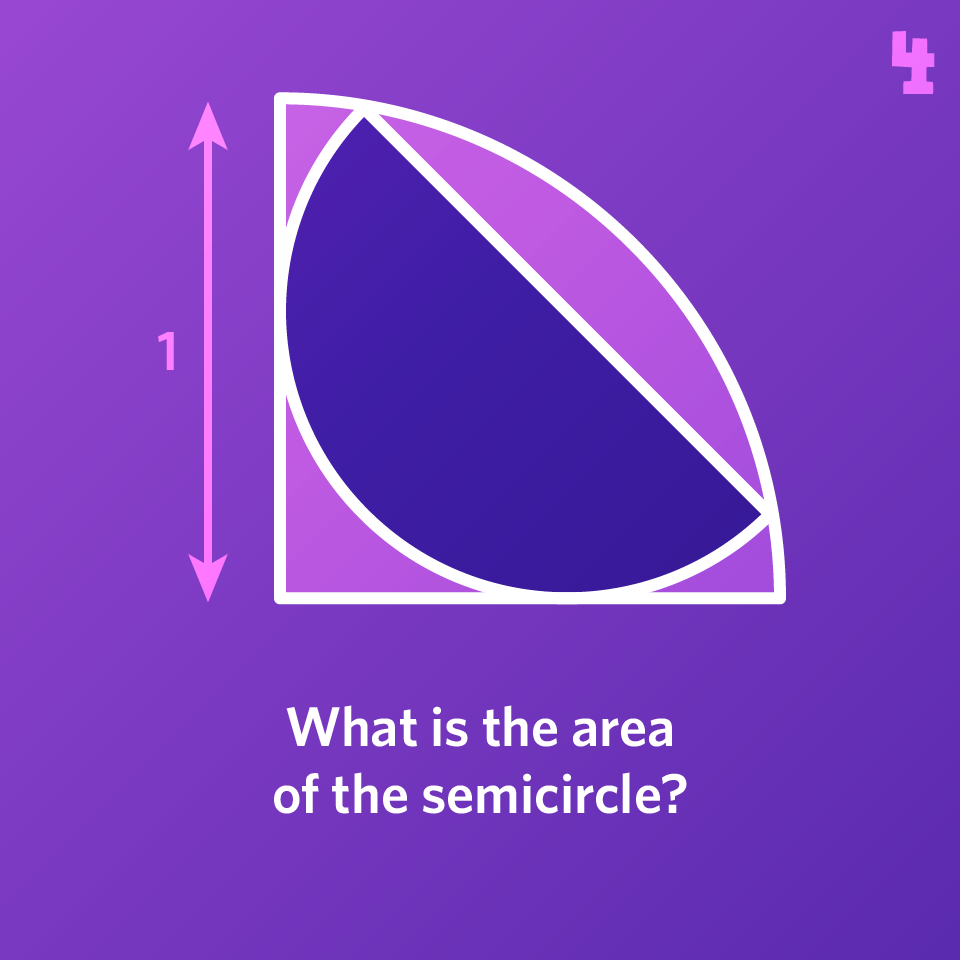
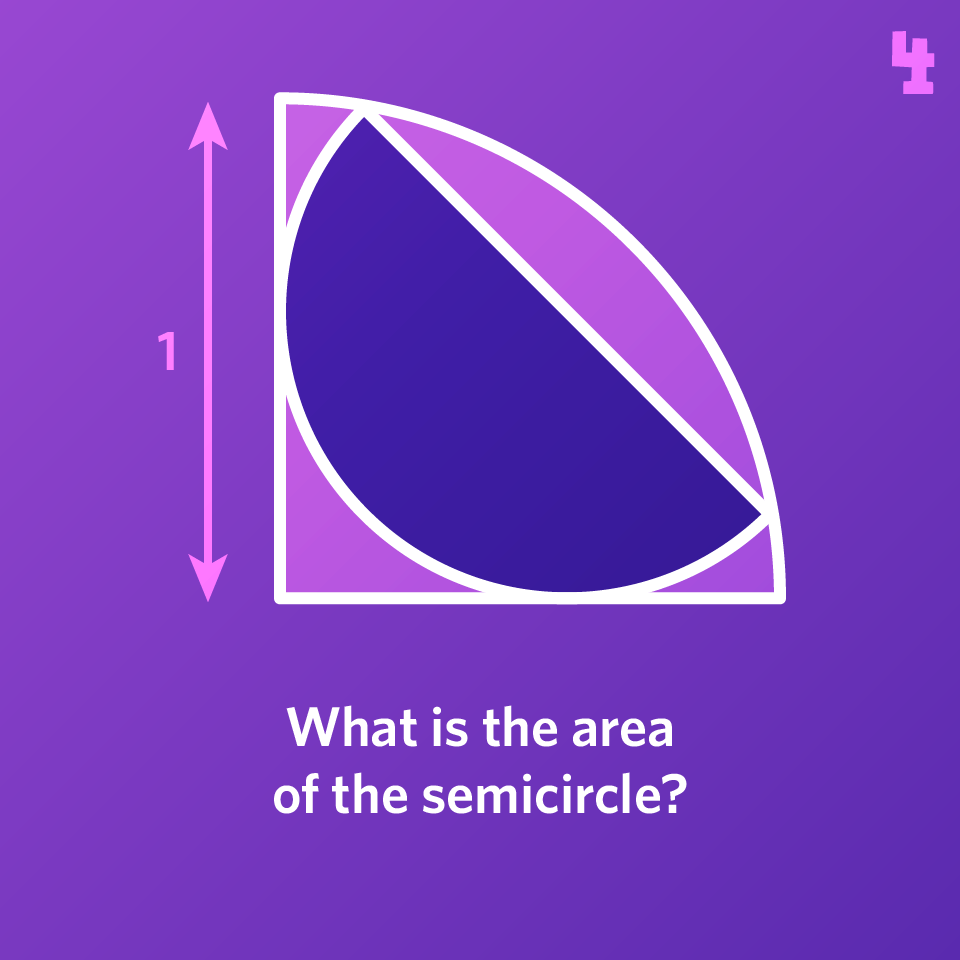
What is the area of the semicircle, which is placed symmetrically inside a quarter circle?

Please sign in to see the solution.

Alice said Bob did it.
Bob said Alice did it.
Carol said Alice didn’t do it.
Dan said it was either Alice or Carol.

Only one person is telling the truth. Who did it?

Please sign in to see the solution.

Can you express 7/8 as a sum of distinct “unit fractions” of the form 1/x?

Please sign in to see the solution.

How many different ways are there to connect four cubes?

Every cube needs to touch at least one other cube, and faces need to line up. You can ignore rotations or reflections.

Please sign in to see the solution.

Can you use eight 8s, together with mathematical symbols like + and –, to make 1000?

Please sign in to see the solution.

What is the ratio of the perimeters of the circumscribed and inscribed hexagon of a circle?

Please sign in to see the solution.

Two athletes are running at constant speeds on a circular track. If they head in opposite directions, they meet after one minute. If they head in the same direction, they meet after one hour. What is the ratio of their speeds?

Please sign in to see the solution.

You have two jugs with volumes 3 and 5 liters, but no markings. Can you use them to get exactly 4 liters of water?

Please sign in to see the solution.

What’s the next number in this sequence?

441, 961, 691, 522, 652, 982, 423, …

Please sign in to see the solution.

A shop sells chocolates in boxes of 6, 9 or 20. What is the largest amount of chocolates that is impossible to buy?

For example, it is impossible to buy 10 chocolates using boxes of 6, 9 or 20.

Please sign in to see the solution.

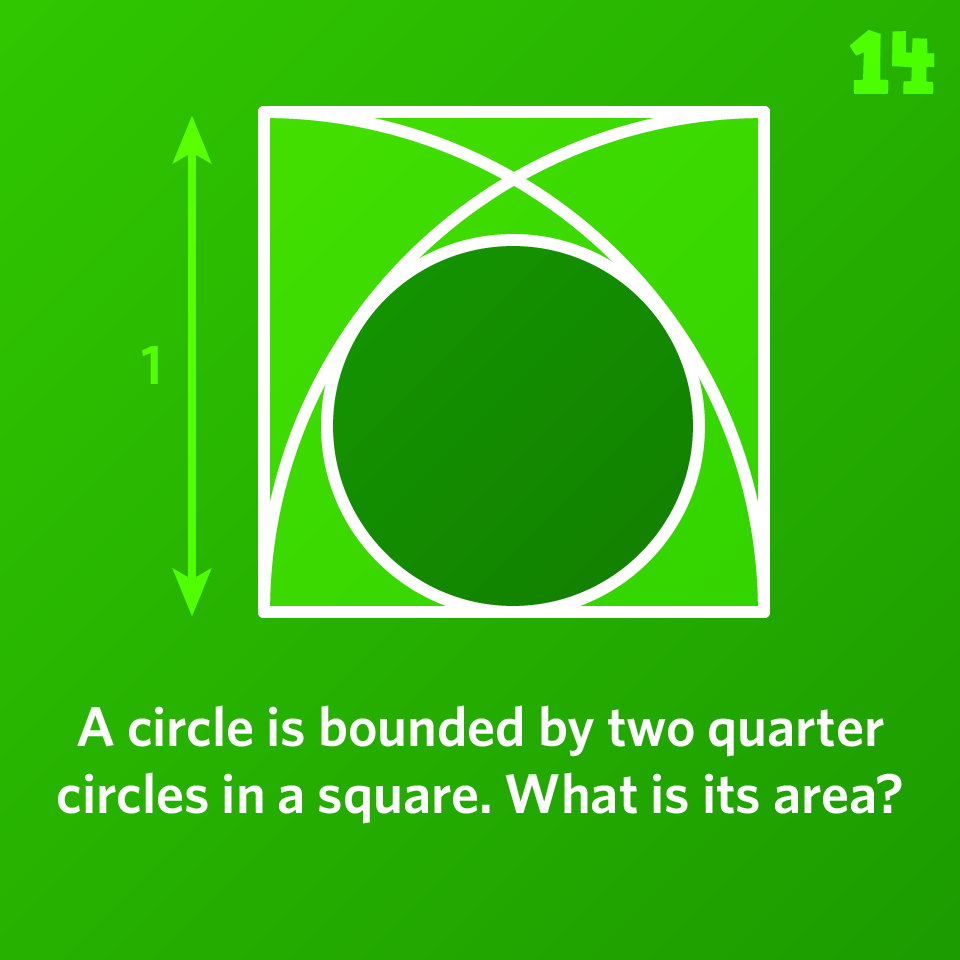
A circle is bounded by two quarter circles in a square. What is its area?

Please sign in to see the solution.

If 5 balls are placed at random into 5 buckets, what is the probability that exactly one bucket remains empty?

Please sign in to see the solution.

How many times per day do the minute and hour hands on a clock form a straight line?

Please sign in to see the solution.

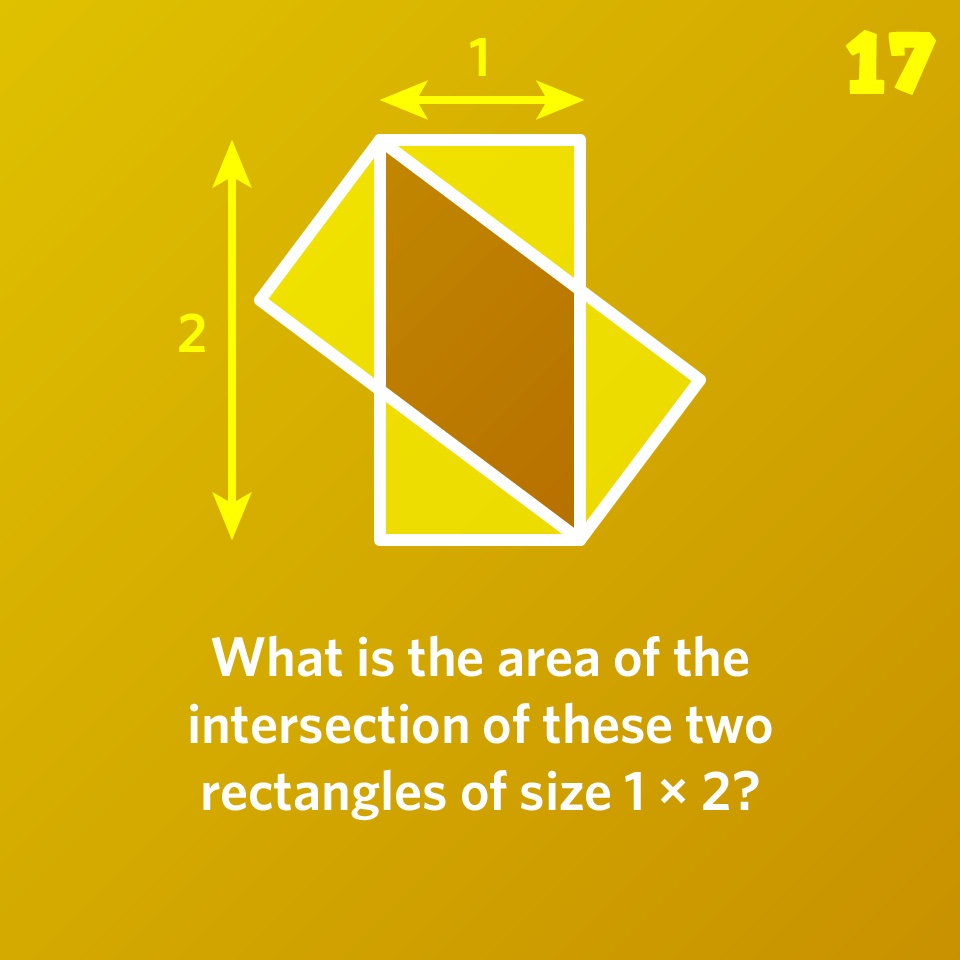
What is the area of the intersection of these two rectangles of size 1 × 2?

Please sign in to see the solution.

What is the sum of the first six cube numbers? What about the first 10 cube numbers?

Please sign in to see the solution.

Can you find a 10-digit number, so that:

• the first digit is the number of zeros in that number,
• second digit is the number of 1s,
• …
• tenth digit is the number of 9s?

Please sign in to see the solution.

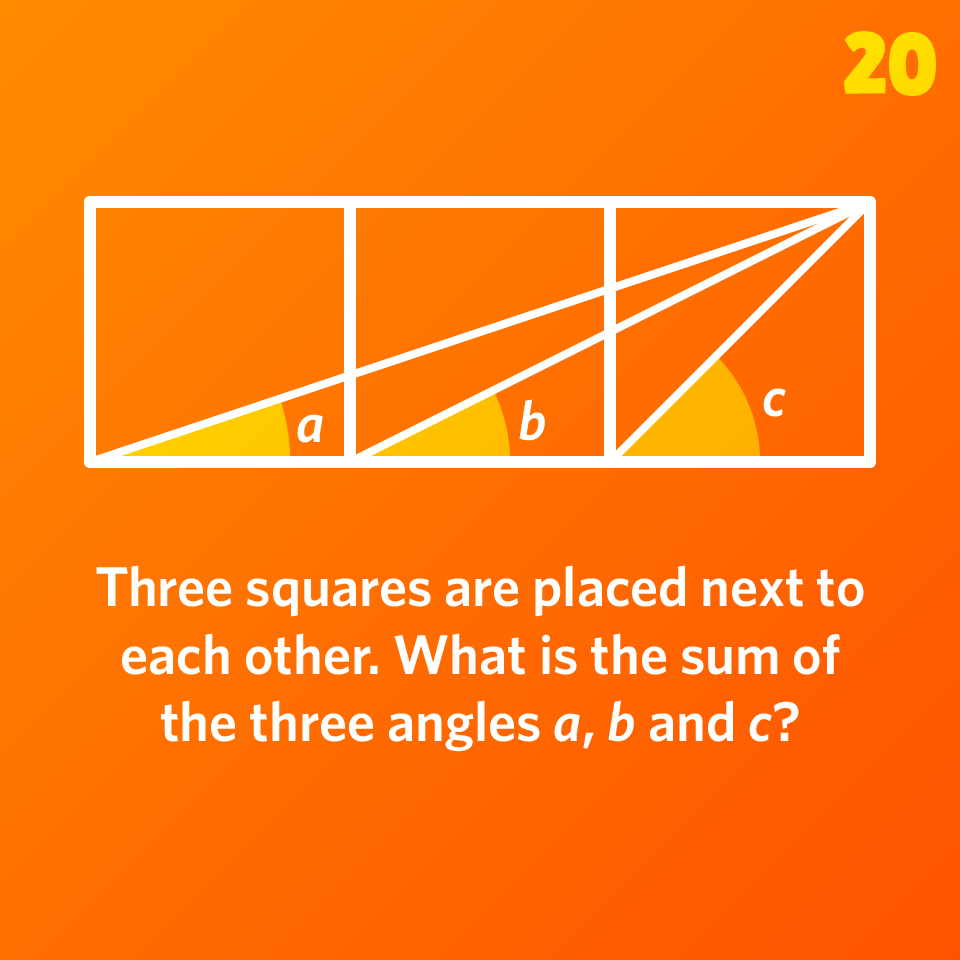
Three squares are placed next to each other. What is the sum of the three angles a, b and c?

Please sign in to see the solution.

How many triangles are in this diagram?

Please sign in to see the solution.

You randomly draw two cards from a standard deck of 52 cards.

What is the probability that both cards have either the same suit or the same number/symbol?

Please sign in to see the solution.

What is the fewest number of weights you need, to be able to balance any weight from 1 to 40 on a 2-sided scale?

Please sign in to see the solution.

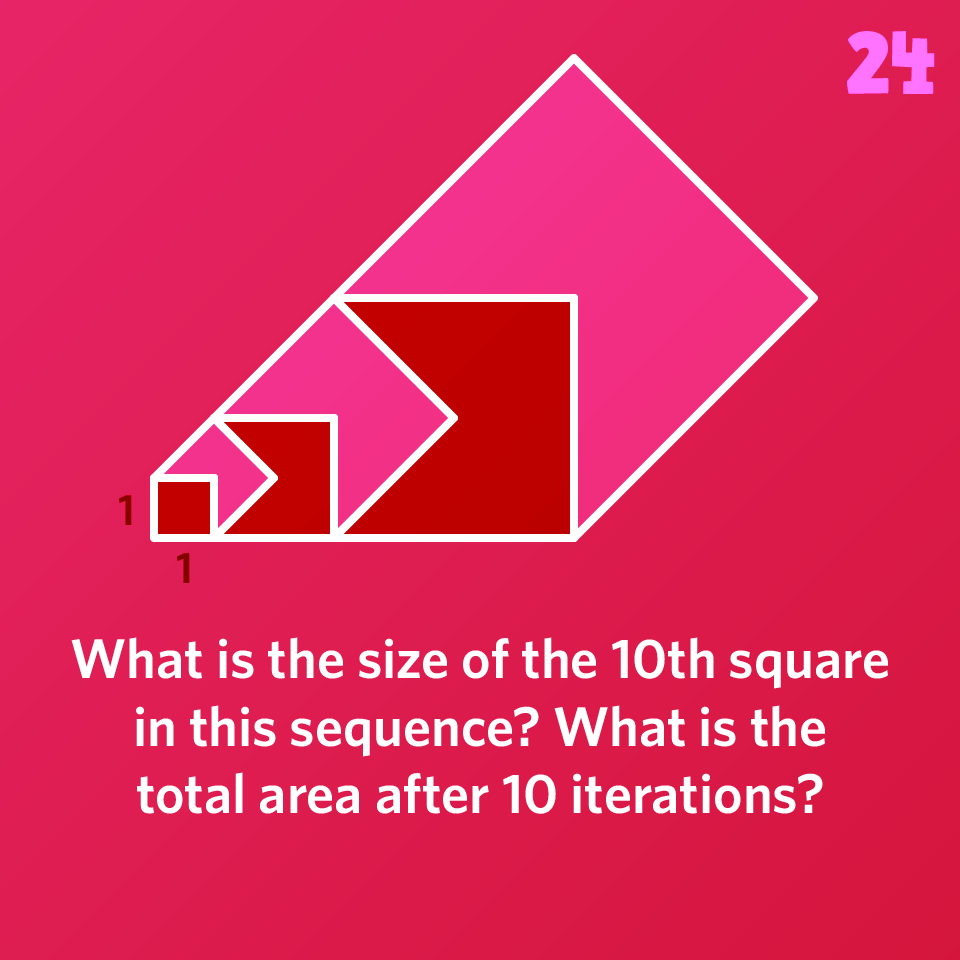
What is the size of the 10th square in this sequence? What is the total area after 10 iterations?

Please sign in to see the solution.

How many paths through this grid are there from A to B, if you can only move right or down?

Please sign in to see the solution.

What is the radius of the smallest circle that contains three circles of radius 1?

What about 4, 5 or more circles?

Please sign in to see the solution.

A rook and a bishop are randomly placed on a chessboard. What is the probability that one is attacking the other?

Please sign in to see the solution.

After 1 and 36, what is the next number that is both a square number and a triangular number?

Please sign in to see the solution.

Given a random string of n left and n right brackets, how often do you need to cut it into two parts and swap both sides, to make it “algebraically valid”?

Puzzle created by James Tanton

Please sign in to see the solution.

Which shape has a larger perimeter: the square or the circle?

Please sign in to see the solution.

There are 26 red and 26 black cards in a deck. A “run” is a set of consecutive cards of the same colour. What is the expected number of runs in a standard shuffled deck?

Please sign in to see the solution.

Seven different digits are placed in a row. The products of the first three, middle three and last three digits are all equal. What is the middle digit?

Please sign in to see the solution.

How many integers between 1 and 1,000,000 have a sum of digits equal to 16?

Please sign in to see the solution.

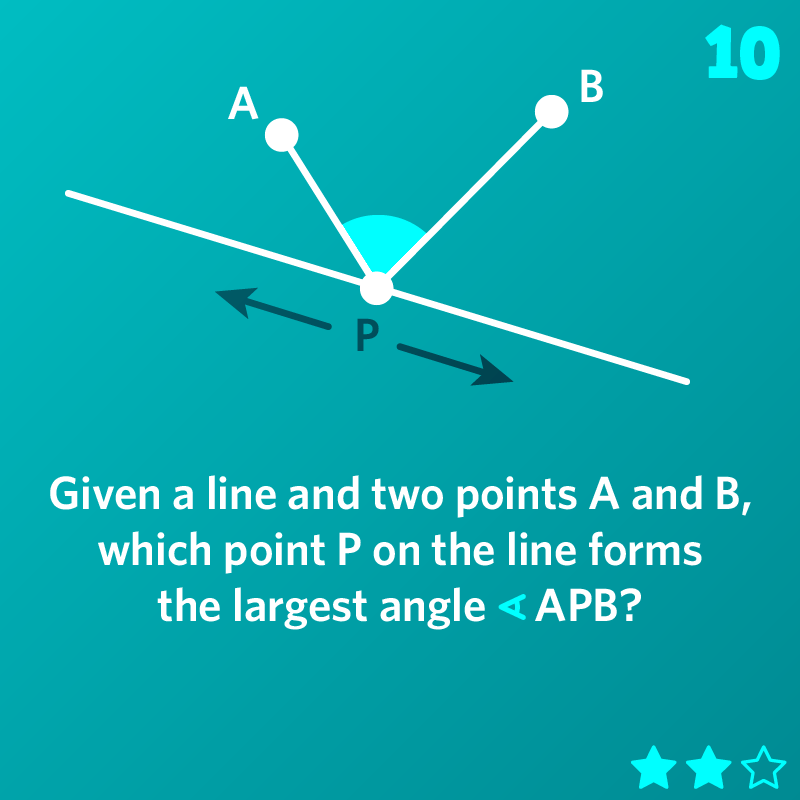
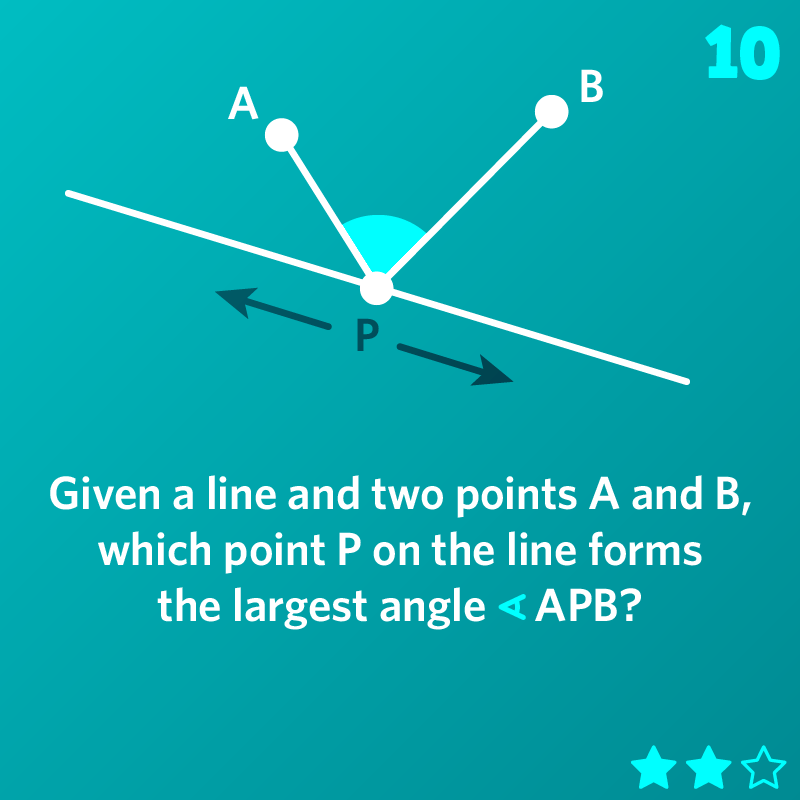
Given a line and two points A and B, which point P on the line forms the largest angle APB?

Puzzle created by James Tanton

Please sign in to see the solution.

Frogs can slide horizontally or vertically by one cell, or jump over one frog horizontally or vertically into an empty space. Can the dark and light frogs switch places?

Puzzle created by James Tanton

Please sign in to see the solution.

Can you find a number that starts with 7 and can be divided by 7 by moving the first 7 to the end?

What about a general approach for any digit?

Please sign in to see the solution.

Five people, A, B, C, D and E, are randomly seated around a circular table. What is the probability that A and B are next to each other?

Can you generalise this to n people?

Please sign in to see the solution.

How do you construct a circle inside another circle, that takes up exactly 1/3 of its area?

Puzzle created by Kiran Bacche

Please sign in to see the solution.

Only one of these statements is true. Which one?

A. All of the below
B. None of the below
C. One of the above
D. All of the above
E. None of the above
F. None of the above

Please sign in to see the solution.

A classic shunting puzzle: can you swap the position of the train cars A and B? The short segment at the top can fit either car, but not the locomotive L.

The locomotive can drive forwards or backwards, and push or pull the cars from either side. You can also connect the two cars to each other.

Please sign in to see the solution.

Two squares of size 20cm are randomly placed inside a larger square of size 1m (edges parallel). What is the probability that the two smaller squares overlap?

Please sign in to see the solution.

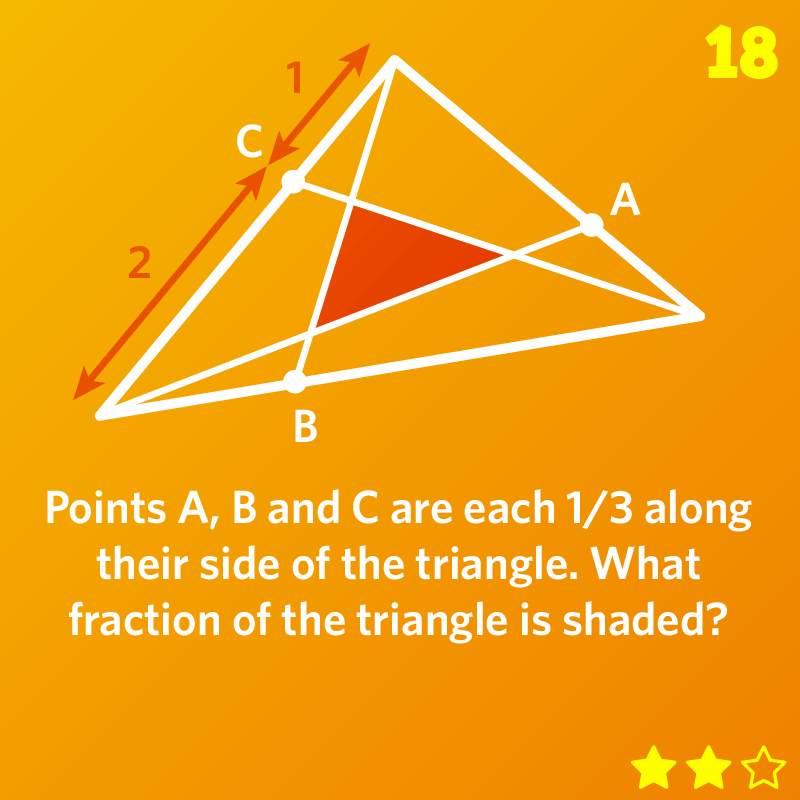
Points A, B and C are each 1/3 along their side of the triangle. What fraction of the triangle is shaded?

Please sign in to see the solution.

A far-away country uses a currency system with just two coins: worth 13 cents and –9 cents respectively. Is it possible to purchase an item that costs 1,568 cents?

Puzzle created by James Tanton

Please sign in to see the solution.

Can you prove that every integer has a multiple that is a Fibonacci number?

How about a (non-zero) multiple that can be written using just 0s and 1s, in base 10?

Please sign in to see the solution.

What proportion of this square, which contains four quarter-circles, is shaded?

Please sign in to see the solution.

How many cards, on average, do you have to draw from a standard shuffled deck (52 cards) until you get the first Ace?

Please sign in to see the solution.

Into how many pieces can you cut a circular pizza with 10 straight cuts from edge to edge?

Pieces don't have to be wedges, or even have the same size.

Please sign in to see the solution.

A group of 20 friends play “Secret Santa”, and draw the name of their target randomly out of a hat.

What is the probability that at least one person draws their own name?

Please sign in to see the solution.

A pandemic is spreading across an n × n grid. Each tile gets “infected” if at least two of its four neighbours are infected. What is the minimum number of infected squares required initially, so that the pandemic could spread to eventually cover the the entire grid?

Please sign in to see the solution.

Six circles with radius 1 are arranged in a regular hexagon. What is the area of the dark, enclosed space?

Please sign in to see the solution.

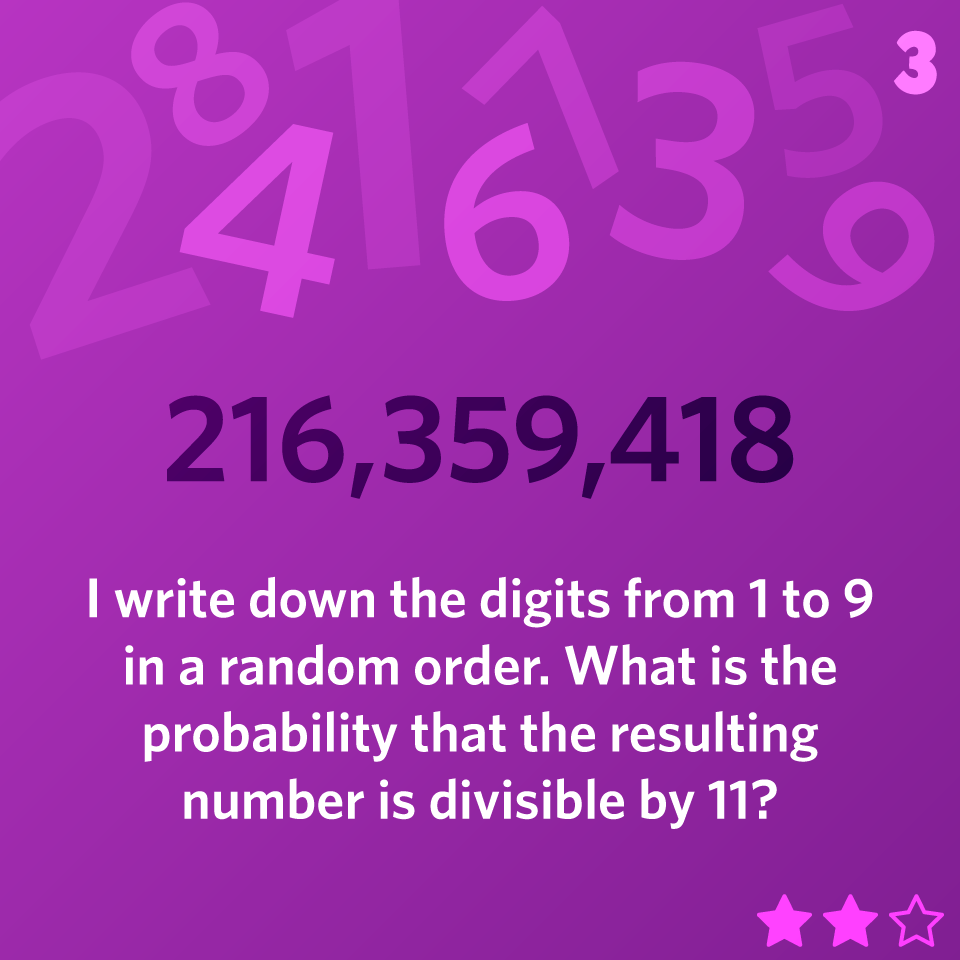
I write down the digits from 1 to 9 in a random order. What is the probability that the resulting number is divisible by 11?

Please sign in to see the solution.

How many squares can you draw with their vertices on a grid?

How about a more general grid?

Please sign in to see the solution.

How often, on average, do you have to roll a die, to see all six sides come up at least once?

Please sign in to see the solution.

An isosceles triangle is placed inside a square. We draw the incircle of the isosceles triangle, and one of the other triangles on either side. What is the ratio of the radii of these two circles?

Please sign in to see the solution.

The numbers a, b, c, d and e are positive integers so that

What is the maximum possible value of any of these integers?

Please sign in to see the solution.

Can you place one star in every row, column and region? Stars can’t be adjacent, even diagonally.

Please sign in to see the solution.

This shape consists of three congruent, right-angled, isosceles triangles. Can you divide it into four congruent regions?

“Congruent” means that the four regions need to have the same size and shape.

Please sign in to see the solution.

Knights always tell the truth and knaves always lie.

You are approached by two of them, and one says “we are both knaves”. Who are they actually?

Please sign in to see the solution.

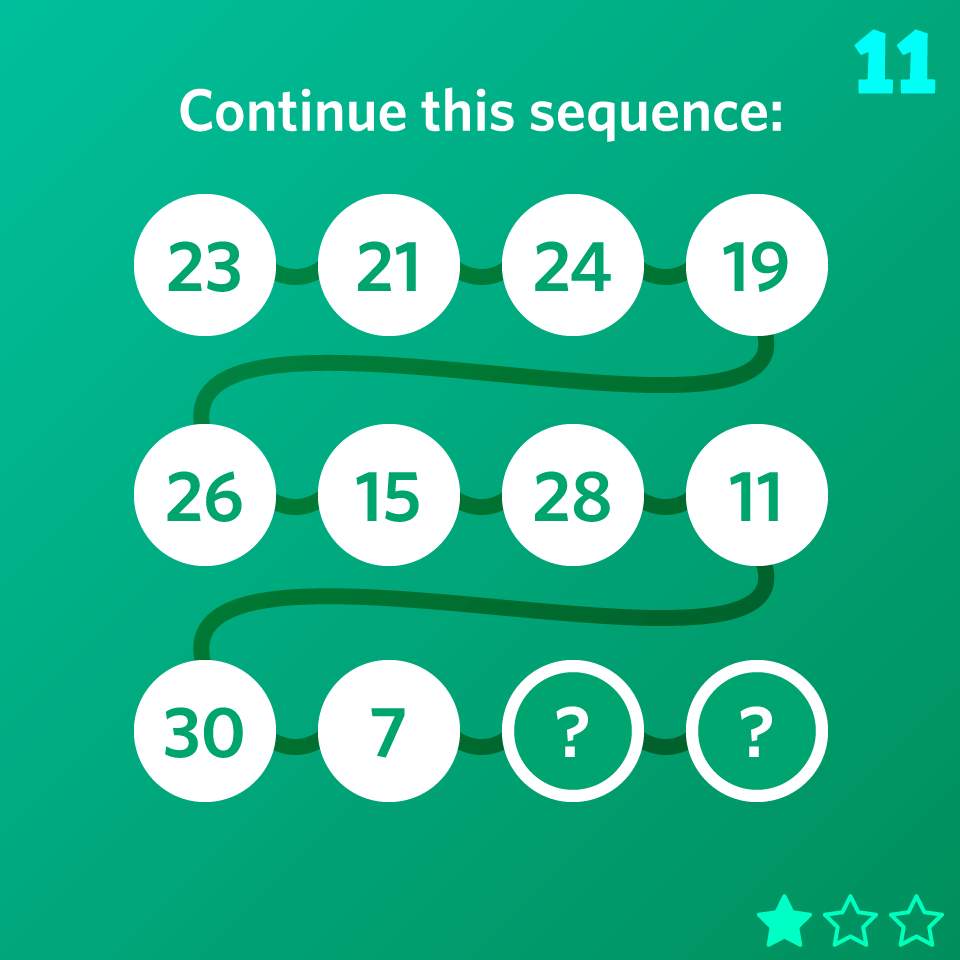
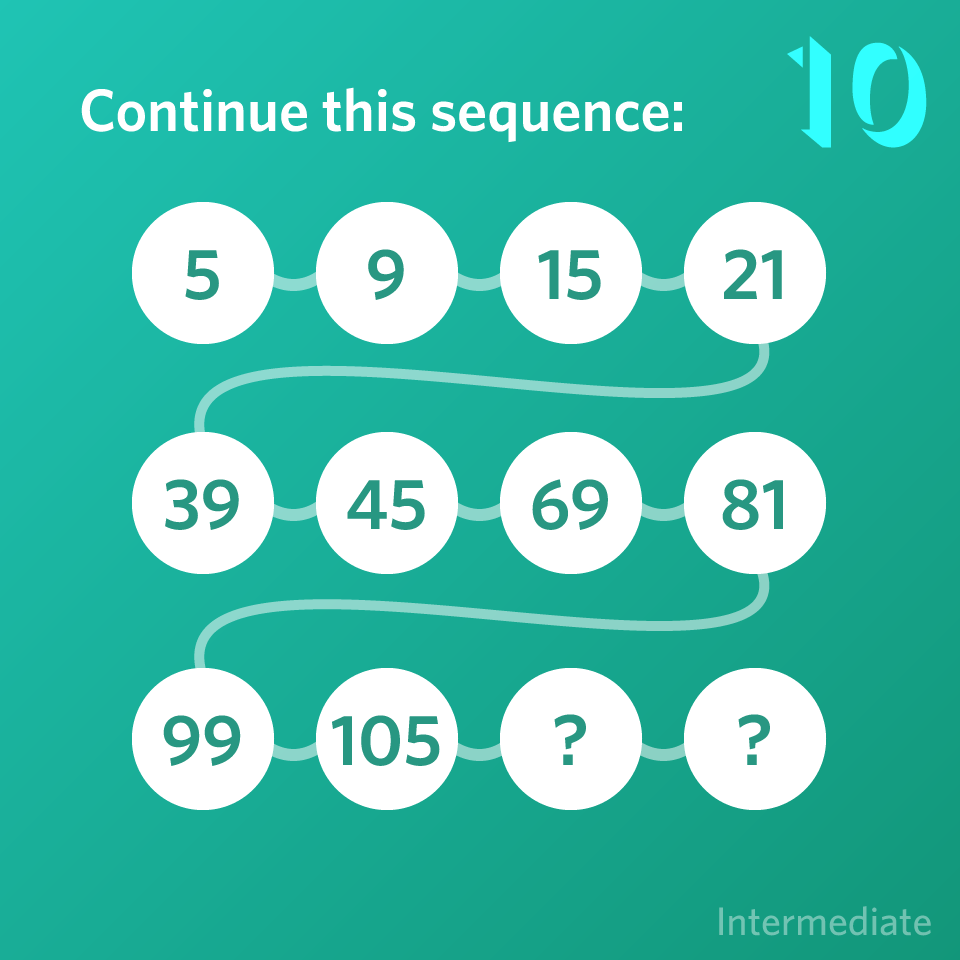
Continue this sequence:

23, 21, 24, 19, 26, 15, 28, 11, 30, 7, ?, ?

Please sign in to see the solution.

What is the radius of the largest circle that can be drawn on a chess board, so that its circumference lies entirely on black squares?

Each square has side length 2.

Please sign in to see the solution.

How far apart are the centres of these two circles with radius 1, if all three shaded regions have the same area?

Please sign in to see the solution.

Can you divide this chessboard into four congruent “kingdoms” that each contain one of the kings? (The kingdoms must have exactly the same size and shape.)

The kings are placed in row 5 and columns 4, 5, 6 and 7, and cannot be moved. The kingdoms also have to be orthogonally connected (they can't consist of multiple disjoint regions).

This puzzle has been featured in The Guardian

Please sign in to see the solution.

A box contains 100 balls labelled from 1 to 100.

You select 10 balls at random. What is the expected value of the largest number you picked?

Please sign in to see the solution.

Place the numbers from 1 to 12 into these circles, arranged in a six-sided star, so that the sum along all six lines is the same.

Please sign in to see the solution.

A white cube is painted black on its outside and then cut into 27 small pieces. The pieces are mixed and randomly reassembled into another cube.

What proportion of the surface area of the new cube is expected to still be black?

Please sign in to see the solution.

A 3-4-5 triangle lies inside a square. What is the area of the square?

Please sign in to see the solution.

Place the digits from 1 to 8 in these boxes, so that consecutive digits are not adjacent (even diagonally).

Please sign in to see the solution.

How often, on average, do you have to flip a (fair) coin, until you get 10 consecutive heads?

Please sign in to see the solution.

Two trains with 2 and 3 carriages are travelling in opposite directions on the same track. There is a siding, but it only has space for one carriage or locomotive. How can the trains pass each other?

Locomotives can drive forwards and backwards, and attach to carriages on either side.

Please sign in to see the solution.

In this triangle, the length of all three sides and its height are four consecutive integers. What is the area of the triangle?

Please sign in to see the solution.

Two 3-digit numbers sum to a third number with 3 digits.

The digits of all three numbers are permutations of each other. What are these numbers?

None of the digits are 0s.

Please sign in to see the solution.

What is the average distance between two points picked randomly on the circumference of a circle?

Note: This problem requires calculus.

Please sign in to see the solution.

This is the most efficient way to place three congruent squares in an equilateral triangle. What proportion of the triangle is shaded?

Please sign in to see the solution.

You pick three random points on a circle. What is the probability that the resulting triangle contains the center of the circle?

The points are picked uniformly at random, along the circumference of the circle.

Please sign in to see the solution.

Can you measure exactly 15 minutes using nothing but an 11-minute hourglass and a 7-minute hourglass?

Please sign in to see the solution.

What proportion of a square is closer to its centre than its edge?

This problem is surprisingly difficult and requires calculus.

Please sign in to see the solution.

What 4-digit number, when multiplied by 4, reverses the order of its digits?

ABCD × 4 = DCBA

This puzzle has been featured in The Guardian

Please sign in to see the solution.

Can you place 18 black and 18 white tiles on a 6×6 board, so that there are no “squares” with their four corners having the same colour?

From Martin Gardner’s “Sphere Packing, Lewis Carroll, and Reversi”

Please sign in to see the solution.

Three geysers A, B and C in a national park erupt every 1, 2 and 3 hours respectively. You just arrived: what is the probability that you will see geyser A erupt first?

Inspired by The Riddler on FiveThirtyEight

Please sign in to see the solution.

What’s the angle between these two congruent equilateral triangles?

Inspired by Catriona Shearer

Please sign in to see the solution.

Continue this sequence:

6, 10, 14, 15, 21, 22, 26, 33, 34, 35, …

Please sign in to see the solution.

Scientists are studying a micro-organism, starting with a single cell. Every day, each cell either splits in two (with probability p), or it dies. What is the probability that the entire organism dies eventually?

Please sign in to see the solution.

Can you arrange the seven Tetrominoes in a 7×4 rectangle, with no gaps or overlaps?

Please sign in to see the solution.

You have 10 cans of peas. All peas weigh 1 gram, except for one can with peas that weigh 0.9 grams. How often do you need to use a scale to find this lighter can?

Please sign in to see the solution.

Can the locomotive L switch the position of the two wagons and end up where it started? Only the locomotive can fit under the bridge.

From Martin Gardner’s “Sphere Packing, Lewis Carroll, and Reversi”

Please sign in to see the solution.

25 frogs are sitting in a 5×5 grid. Every frog jumps into an adjacent square (left, right, up or down). What is the largest number of squares that could become empty?

This puzzle has been featured in The Guardian

From the Netherlands Junior Maths Olympiad

Please sign in to see the solution.

I repeatedly toss a fair coin and record the outcome. What is the probability that the sequence “HHH” occurs before “THH”?

Please sign in to see the solution.

A castle is surrounded by a 5 meter wide, rectangular moat. Can you cross it using nothing except two planks that are 4.8 meters long?

This puzzle has been featured in The Guardian

Please sign in to see the solution.

What’s the value of x?

x^xxxx… = 2

Please sign in to see the solution.

Can you plant 7 trees so that there are 6 straight lines containing 3 trees each?

Please sign in to see the solution.

How many ways are there to distribute 10 identical cookies between five different kids?

Kids don’t need to receive the same number of, or any, cookies.

Please sign in to see the solution.

What is the least number of integers needed, so that any of these could be true?

Median < Mean < Mode
Median < Mode < Mean
Mode < Median < Mean
Mode < Mean < Median
Mean < Mode < Median
Mean < Median < Mode

The mode has to be well-defined, so you can’t have two different integers both appear the most number of times. For example, the set {1, 2, 2, 3, 3} doesn’t have a well-defined mode, because both 2 and 3 appear twice.

Please sign in to see the solution.

Rearrange these numbers and symbols to make a true equation:

2 3 4 5 + =

Please sign in to see the solution.

There are 100 strings in a bag. You randomly pick two ends and tie them together, until there are no free ends left. What is the expected number of loops you will create?

Please sign in to see the solution.

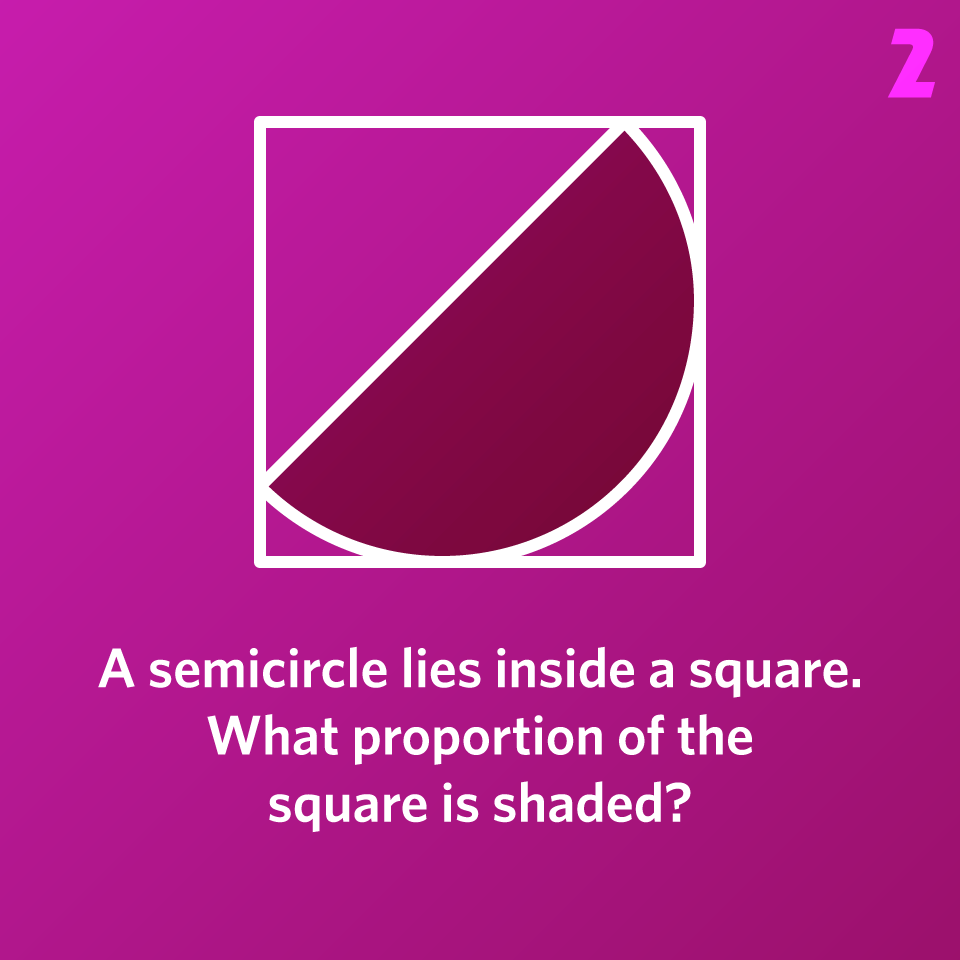
A semicircle lies inside a square. What proportion of the square is shaded?

Please sign in to see the solution.

How many ways are there to tile a rectangle of size 2×10 with dominoes?

Dominoes are tiles of size 2×1 and can be placed horizontally or vertically. All dominoes need to be contained within the board, and there can’t be any gaps. Can you find a general answer for a board of size 2×n? What about a board of size 3×n?

Please sign in to see the solution.

How many triangles are there?

This puzzle has been featured in The Guardian

Please sign in to see the solution.

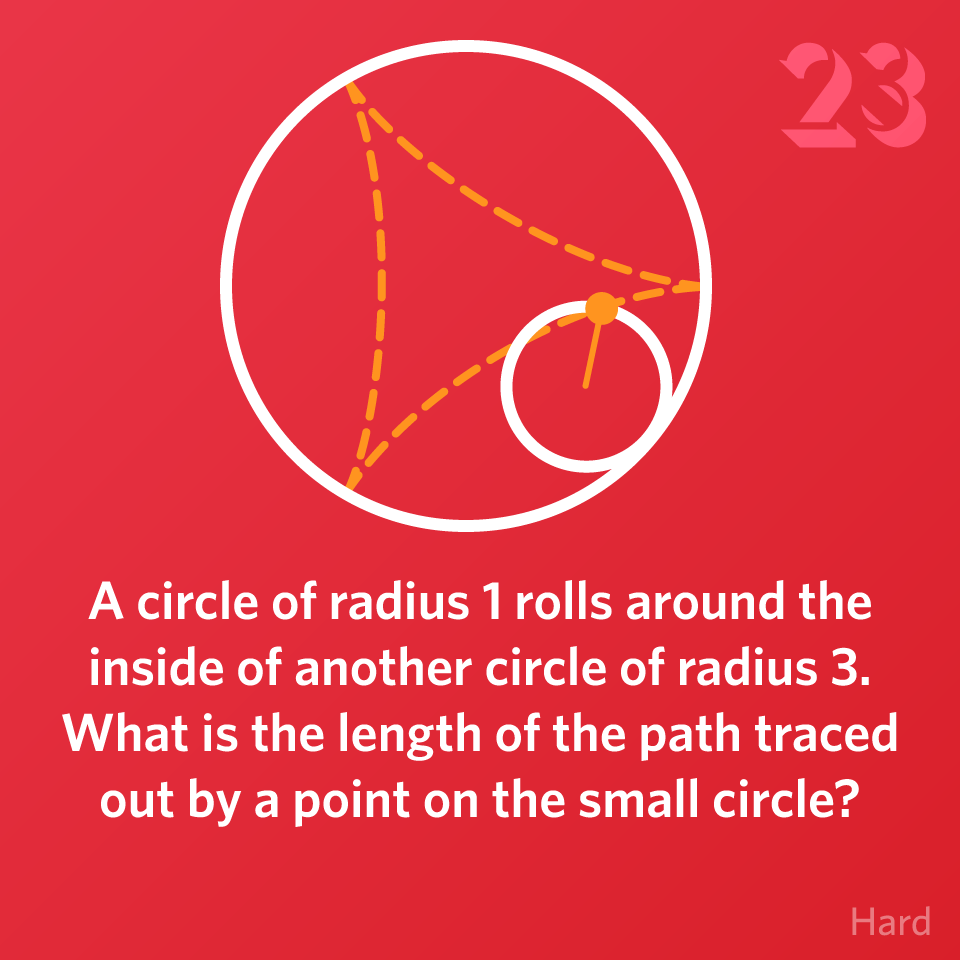
A circle of radius 1 rolls around the inside of another circle of radius 3. What is the length of the path traced out by a point on the small circle?

Please sign in to see the solution.

I’m thinking about a large integer.

• It is divisible by 1.
• It is divisible by 2.
• It is divisible by 3.
• …
• It is divisible by 30.

Exactly two consecutive of these statements are wrong. Which ones?

This puzzle has been featured in The Guardian

Please sign in to see the solution.

You have 9 balls, one of which is slightly heavier than the others.

How often do you need to weigh two groups of balls, to find the odd one out?

Please sign in to see the solution.

Two equilateral triangles are drawn inside a square. What is the area of the smaller triangle?

Please sign in to see the solution.

A cinema announces a special deal: the first person in the queue to have the same birthday as someone in front of them, will get a free ticket.

Which position in the queue is the best?

Please sign in to see the solution.

At a party, every guest shook hands with everyone else. There were 66 Handshakes in total. How many guests attended the party?

Please sign in to see the solution.

Four cities form the vertices of a square. What is the shortest way to connect them with each other using railroad tracks?

The tracks may intersect, and you can add “junctions”. Hint: Two diagonals is not the shortest path!

Please sign in to see the solution.

This is a Magic Sum Square, where the sum of every row, column and diagonal is 15. Can you find a Magic Product Square?

Please sign in to see the solution.

Can you cut this obtuse triangle into smaller, acute triangles? If so, how many cuts do you need?

Note that a right angle is neither acute nor obtuse!

Please sign in to see the solution.

A cylindrical hole of length 6cm has been drilled through the center of a solid sphere. What is the volume of the remaining sphere?

Please sign in to see the solution.

When placing 5 queens on a 5µ5 chess board, what is the maxiumum number of fields you can leave “unattacked” (no queen can reach them within one turn)?

This puzzle has been featured in The Guardian

Please sign in to see the solution.

Can you insert mathematical operators, to make this equation true?

0 0 0 0 0 = 120

Please sign in to see the solution.

Where did the missing square go?

Please sign in to see the solution.

Continue this sequence:

5, 9, 15, 21, 39, 45, 69, 81, 99, 105, …

Please sign in to see the solution.

I’ll offer you $4 to play this game:

You have to toss a coin repeatedly, until it lands heads. Then you have to pay me back $1 for every toss.

Do you want to play?

Please sign in to see the solution.

You have two ropes that burn in exactly 60 minutes – but not neccessarily at a constant rate.

How can you measure 45 minutes?

Please sign in to see the solution.

A farmer has 300 bananas which he wants to sell at a market 100km away.

His camel can carry 100 bananas at once, and eats one banana per km.

What is the most bananas he can take to the market?

Please sign in to see the solution.

How many guards do you need for this museum, so that every corner can be watched?

Guards have 360° vision, but they cannot move.

Please sign in to see the solution.

Here you can see some examples of Trapezium Numbers. There is just one number between 1,000 and 2,000 that doesn’t form a trapezium. Which one?

Please sign in to see the solution.

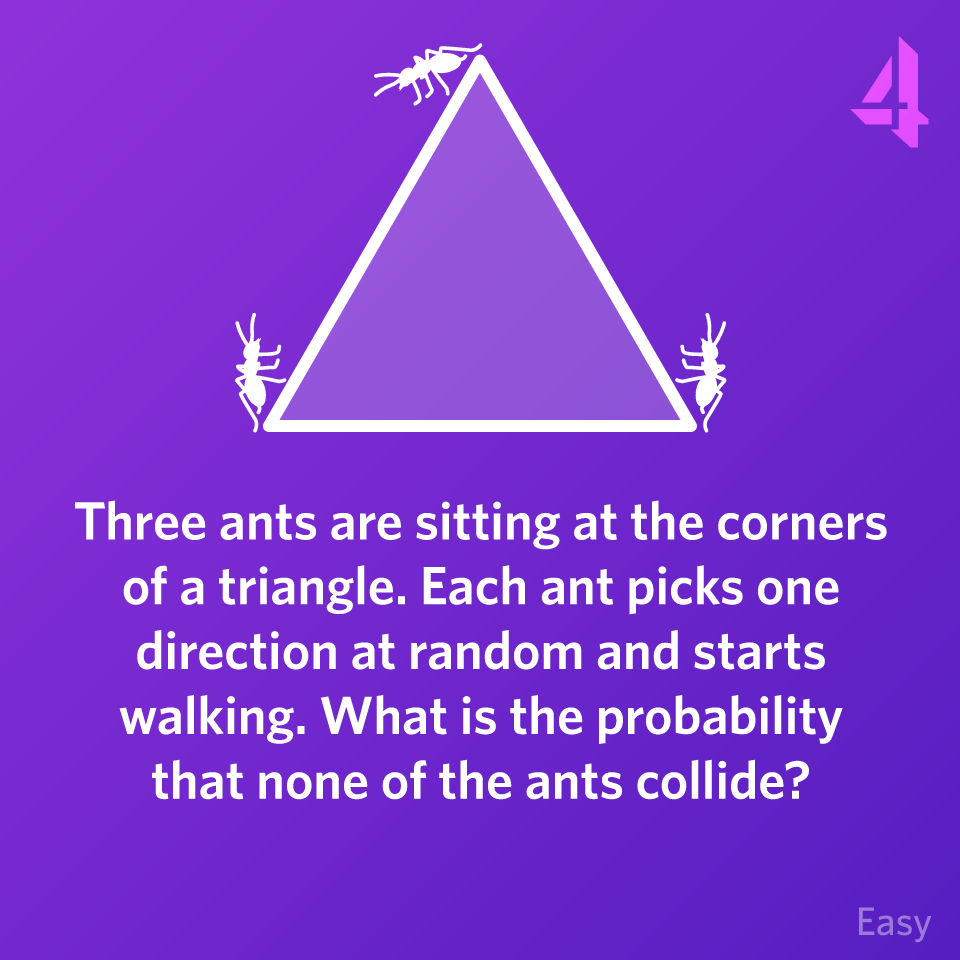
Three ants are sitting at the corners of a triangle. Each ant picks one direction at random and starts walking. What is the probability that none of the ants collide?

This puzzle has been featured in The Guardian

Please sign in to see the solution.

You break a stick in two different places at random. What is the probability that the resulting three pieces form a triangle?

Please sign in to see the solution.

You have a large number of 5-cent stamps and 17-cent stamps. What is the largest cent value which you cannot make using a combination of these stamps?

Please sign in to see the solution.

Which regular polygons can be created using a ring of other regular polygons?

Please sign in to see the solution.

Can you make 24 using the numbers

3, 3, 8, 8,

and the operations

+ – × ÷ ( )

How many people do you need, so that the probability of two having the same birthday is at least 50%

A bag contains two green marbles and two blue marbles.

I pick two marbles at random and tell you that at least one is blue. What is the probability that the other one is also blue?

A small country contains 10 cities and 5 straight roads. Every road connects 4 different cities. Draw a map of the country!

How many guests do I have to invite to my christmas party, to be sure there will be at least 3 mutual friends, or 3 mutual strangers?

Any two guests are either strangers or friends.

In a dark room there’s a drawer with 10 red socks and 10 blue socks. How many socks do you have to take, to be sure to get a matching pair?

A market stall sells five different kinds of fruit.

I want to buy ten items. How many possible combinations are there?

How can I measure exactly 8 liters of water, using just one 11 liter and one 6 liter bucket?

People from the Town of Truth always tell the truth. People from the City of Lies always lie.

A guide from one of the cities is at the intersection and offers you a single question. What should you ask?

Place the numbers from 1 to 9 in the circles, so that the sum along all 3 sides is the same.

How many triangles are there?

You have to deliver five letters to five different houses, but the rain has erased all addresses. If you just distribute the letters randomly, what is the probability that everyone gets a wrong letter?

How many diagonals are there in a 10-gon?

What’s the smallest set of integers a, b, c, d and e that satisfy

a + b = c + d + e AND a² + b² = c² + d² + e²

All shapes have the same perimeter. Which one has the largest area?

Is the yellow dot on the inside or the ouside of this spiral?

Can you split this shape into two equal parts, with a single cut?

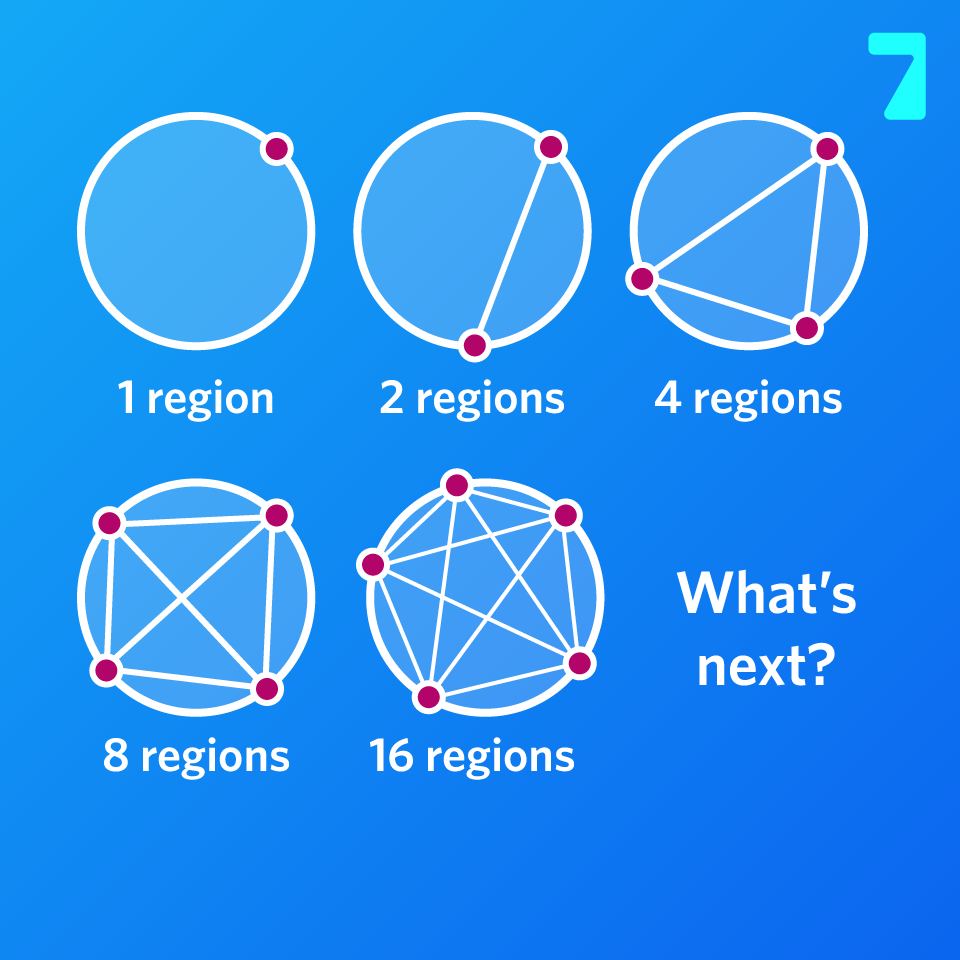
What’s next?

Where did the missing square go?

Find all pairs of numbers a and b that satisfy:

a + b = a × b = a / b.

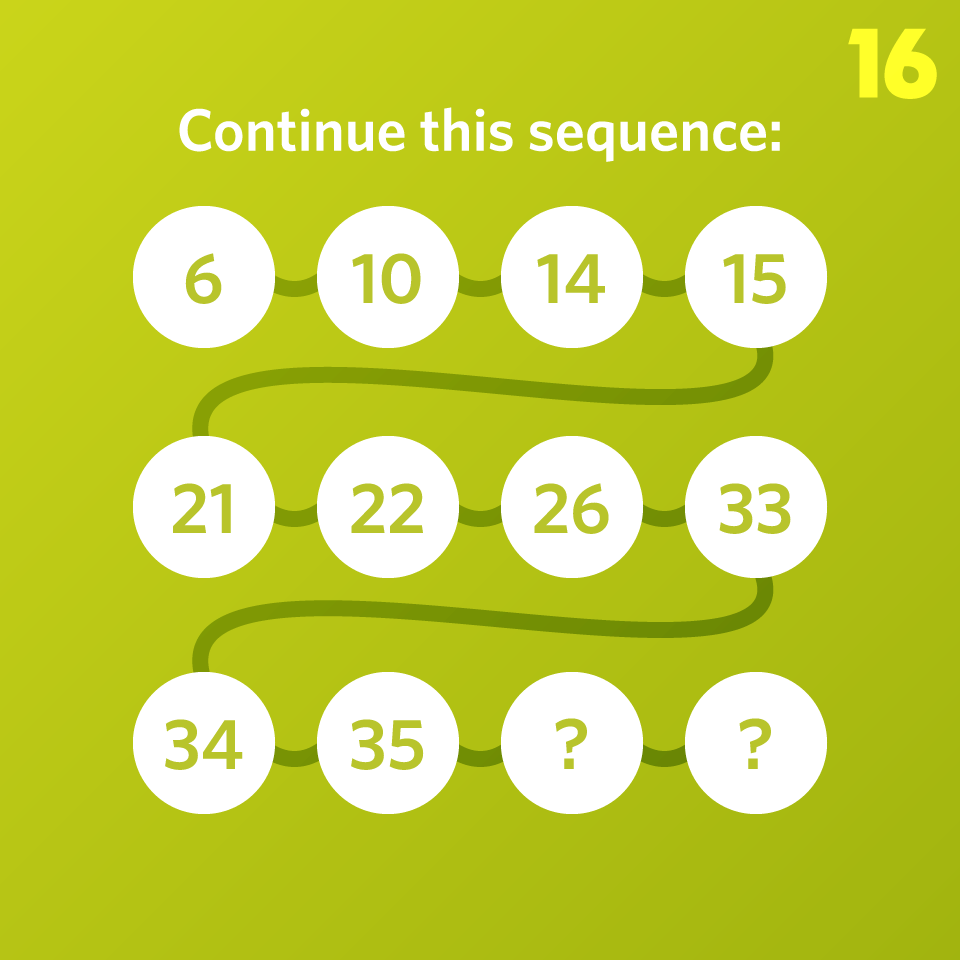
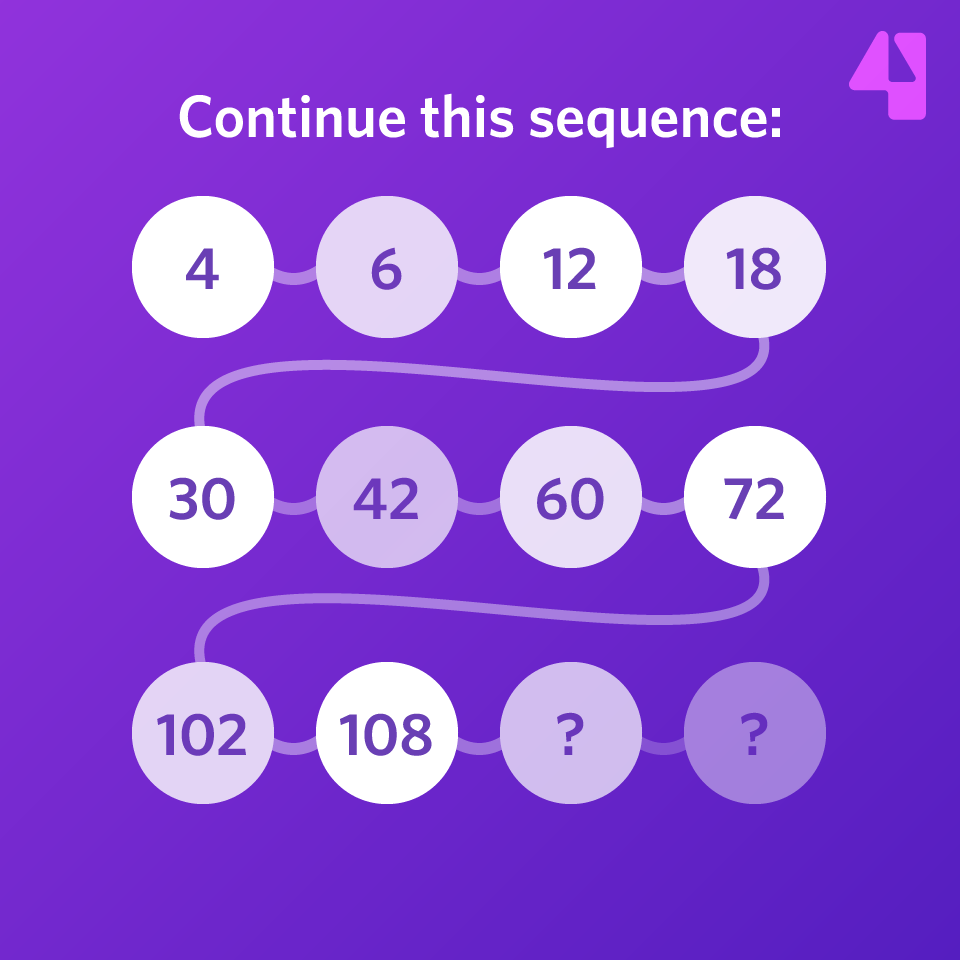
Continue this sequence:

4, 6, 12, 18, 30, 42, 60, 72, 102, 108, …

What’s the area of the Koch Snowflake, where the largest triangle has side length 1?

Can you cover a 8×8 chessboard, with the two opposite corner tiles removed, entirely with dominoes (no gaps or overlaps)?

Rearrange these seven shapes to form the animals above!