Transformaciones y SimetríaGrupos de simetría y fondos de pantalla
Algunas formas tienen más de una simetría: echemos un vistazo al








Ya has mostrado anteriormente que un cuadrado tiene
También tiene simetría rotacional en
Y finalmente, podemos pensar en "no hacer nada" como otro tipo especial de simetría, porque el resultado es (obviamente) el mismo que antes. Esto a veces se llama identidad .
En total, hemos encontrado
Ahora podemos comenzar a hacer algo de aritmética con estas simetrías. Por ejemplo, podemos agregar dos simetrías para obtener otras nuevas:






Cada vez que agrega dos simetrías de un cuadrado, obtiene una nueva. Aquí hay una "calculadora de simetría" donde puede probarla usted mismo:
Pasa un tiempo jugando con la calculadora de simetría e intenta encontrar cualquier patrón. ¿Puedes completar estas observaciones?
- Agregar dos rotaciones siempre dará
(o la identidad). * Agregar dos reflexiones siempre dará (o la identidad). * Agregar las mismas dos simetrías en el orden opuesto a resultado. * Agregar la identidad .
Es posible que ya te hayas dado cuenta de que agregar simetrías es en realidad muy similar a agregar enteros :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
En matemáticas, cualquier colección que tenga estas propiedades se llama
En este ejemplo, comenzamos con las ocho simetrías del cuadrado. De hecho, cada forma geométrica tiene su propio grupo de simetría . Todos tienen elementos diferentes, pero siempre satisfacen las tres reglas anteriores.
Los grupos aparecen en todas partes en matemáticas. Los elementos pueden ser números o simetrías, pero también polinomios, permutaciones, matrices, funciones ... cualquier cosa que obedezca las tres reglas. La idea clave de la teoría de grupos es que no estamos interesados en los elementos individuales, solo en cómo interactúan entre sí .
Por ejemplo, los grupos de simetría de diferentes moléculas pueden ayudar a los científicos a predecir y explicar las propiedades de los materiales correspondientes.
Los grupos también se pueden utilizar para analizar la estrategia ganadora en los juegos de mesa, el comportamiento de los virus en la medicina, las diferentes armonías en la música y muchos otros conceptos ...
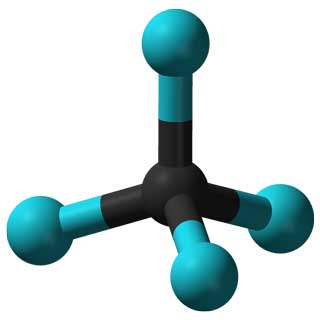
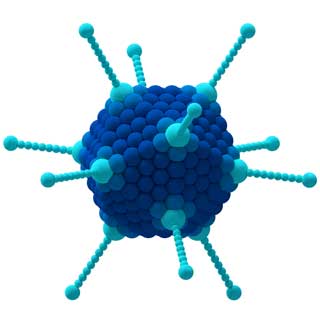
Las propiedades de la molécula CCl 4 (izquierda) y el adenovirus (derecha) están determinadas por sus simetrías.
Grupos de papel tapiz
En las secciones anteriores vimos dos tipos diferentes de simetría correspondientes a dos transformaciones diferentes: rotaciones y reflexiones. Pero también hay una simetría para el tercer tipo de transformación rígida: las


Honyecomb hexagonal


Revestimiento cerámico
Además de la simetría de reflexión, rotación y traslación, incluso hay un cuarto tipo:


Un patrón puede tener más de un tipo de simetría. Y al igual que para los cuadrados, podemos encontrar el
Estos grupos no le dicen mucho sobre cómo se ve el patrón (por ejemplo, sus colores y formas), sino cómo se repite . Múltiples patrones diferentes pueden tener el mismo grupo de simetría, siempre que se organicen y repitan de la misma manera.


Estos dos patrones tienen las mismas simetrías, a pesar de que se ven muy diferentes. Pero las simetrías no se tratan de colores o formas superficiales.


Estos dos patrones también tienen las mismas simetrías, a pesar de que se parecen más a los patrones correspondientes a la izquierda que a los demás.
Resulta que, si bien hay infinitos patrones posibles, todos tienen uno de solo 17 grupos de simetría diferentes. Estos se llaman los grupos de fondo de pantalla . Cada grupo de fondos de pantalla se define por una combinación de traslaciones, rotaciones, reflejos y reflejos de deslizamiento. ¿Puedes ver los

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
Desafortunadamente, no hay una razón simple por la cual hay 17 de estos grupos, y demostrarlo requiere matemáticas más avanzadas. En su lugar, puede intentar dibujar sus propios patrones repetidos para cada uno de los 17 grupos de fondos de pantalla:
Examples of other students’ drawings



Los grupos de papel tapiz tenían que ver con patrones planos y bidimensionales. Podemos hacer algo similar para los patrones tridimensionales: estos se llaman grupos cristalográficos, ¡y hay 219 de ellos!
Además de las traslaciones, reflexiones, rotaciones y reflejos de deslizamiento, estos grupos incluyen simetrías como planos de deslizamiento y ejes de tornillo (piense en el movimiento al desenroscar una botella).
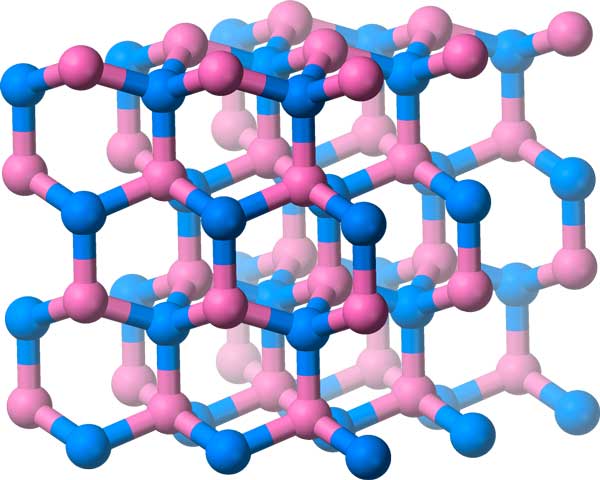
El nitruro de boro tiene sus moléculas dispuestas en esta red cristalina, que tiene un grupo de simetría tridimensional.