Polígonos y PoliedrosTeselaciones

Los polígonos aparecen en todas partes en la naturaleza. Son especialmente útiles si desea enlosar un área grande, porque puede encajar polígonos juntos sin espacios ni superposiciones. Patrones como ese se llaman teselaciones .

Los humanos han copiado muchos de estos patrones naturales en el arte, la arquitectura y la tecnología, desde la antigua Roma hasta el presente. Aquí están algunos ejemplos:

Aquí puede crear sus propios mosaicos utilizando polígonos regulares. Simplemente arrastre nuevas formas desde la barra lateral al lienzo. ¿Qué formas teselan bien? ¿Hay formas que no se tessellate en absoluto? ¡Intenta crear patrones interesantes!

Examples of other students’ tessellations

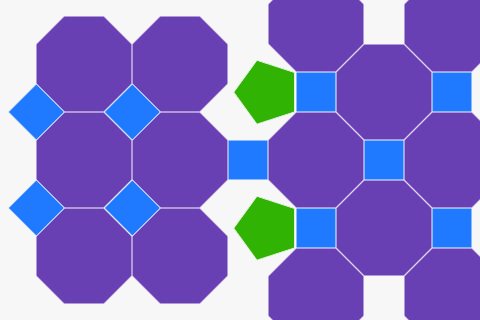
Teselaciones de polígonos regulares

Es posible que haya notado que algunos polígonos regulares (como cuadrados) pentágonos ) se teselan muy fácilmente, mientras que otros (como los pentágonos triangulos hexágonos ) no parecen teselar en absoluto.

Esto tiene que ver con el tamaño de sus ángulos internos , que aprendimos a calcular antes. En cada vértice de la teselación, se encuentran los ángulos internos de múltiples polígonos diferentes. Necesitamos todos estos ángulos para sumar °, de lo contrario habrá un espacio o una superposición.

De manera similar, puede verificar que, al igual que los pentágonos, cualquier polígono regular con 7 o más lados no se teselelate. ¡Esto significa que los únicos polígonos regulares que se teselan son triángulos, cuadrados y hexágonos!

Por supuesto, puede combinar diferentes tipos de polígonos regulares en una teselación, siempre que sus ángulos internos puedan sumar 360°:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

Teselaciones de polígonos irregulares

También podemos intentar hacer mosaicos con polígonos irregulares , siempre que tengamos cuidado al rotarlos y organizarlos.

Los pentágonos son un poco más complicados. Ya vimos que los pentágonos regulares no se teselan teselado , pero ¿qué pasa con los no regulares?

Aquí hay tres ejemplos diferentes de teselaciones con pentágonos. No son regulares , pero son polígonos de 5 lados perfectamente válidos.

Hasta ahora, los matemáticos solo han encontrado 15 tipos diferentes de teselaciones con pentágonos (convexos), el más reciente de los cuales se descubrió en 2015. Nadie sabe si hay otros, o si estos 15 son los únicos ...

Teselaciones en el arte

Tessellations es a la vez una herramienta e inspiración para muchos artistas, arquitectos y diseñadores, especialmente el artista holandés MC Escher . El trabajo de Escher contiene criaturas, patrones y paisajes extraños y mutantes:

Estas obras de arte a menudo se ven divertidas y sin esfuerzo, pero los principios matemáticos subyacentes son los mismos que antes: ángulos, rotaciones, traslaciones y polígonos. Si las matemáticas no están bien, ¡la teselación no funcionará!

“Metamorphosis II” by M. C. Escher (1940)

Penrose Tilings

Todas las teselaciones que vimos hasta ahora tienen una cosa en común: son periódicas . Eso significa que consisten en un patrón regular que se repite una y otra vez. Pueden continuar para siempre en todas las direcciones y se verán igual en todas partes.

En la década de 1970, el matemático y físico británico Roger Penrose descubrió teselaciones no periódicas : todavía continúan infinitamente en todas las direcciones, pero nunca se ven exactamente iguales. Estos se llaman inclinaciones de Penrose , y solo necesita unos pocos tipos diferentes de polígonos para crear uno:

Penrose estaba explorando los mosaicos puramente por diversión, pero resulta que la estructura interna de algunos materiales reales (como el aluminio) sigue un patrón similar. El patrón incluso se usó en papel higiénico, porque los fabricantes notaron que un patrón no periódico puede enrollarse sin abultamientos.