Polígonos y PoliedrosSólidos platónicos

Al comienzo de este curso definimos polígonos regulares como polígonos particularmente "simétricos", donde todos los lados y ángulos son iguales. Podemos hacer algo similar para los poliedros.

En un poliedro regular, todas las caras son del mismo tipo de polígono regular, y la misma cantidad de caras se encuentran en cada vértice . Los poliedros con estas dos propiedades se llaman sólidos platónicos , llamados así por el filósofo griego Platón .

Entonces, ¿cómo son los sólidos platónicos y cuántos de ellos hay? Para hacer una forma tridimensional, necesitamos al menos caras para encontrarse en cada vértice. Comencemos sistemáticamente con el polígono regular más pequeño: triángulos equiláteros:

Y siete o más triángulos en cada vértice tampoco producen nuevos poliedros: no hay suficiente espacio alrededor de un vértice, para acomodar tantos triángulos.

Esto significa que hemos encontrado sólidos platónicos que consisten en triángulos. Pasemos al siguiente polígono regular: cuadrados.

A continuación, intentemos con pentágonos regulares:

Si pentágonos se encuentran en cada vértice, obtenemos el Dodecaedro . Tiene caras. ("Dodeca" significa "doce" en griego).

El siguiente polígono regular para probar son los hexágonos:

Si tres hexágonos se encuentran en cada vértice, inmediatamente obtenemos un mosaico poliedro hexaedro Dado que no hay espacio para más de tres, parece que no hay sólidos platónicos que consisten en hexágonos.

Lo mismo también ocurre para todos los polígonos regulares con más de seis lados. No se teselan, y ciertamente no obtenemos ningún polígono tridimensional.

¡Esto significa que solo hay sólidos platónicos! Echemos un vistazo a todos ellos juntos:

Observe cómo se el número de caras y vértices lo mismo para el cubo y el octaedro , así como para el dodecaedro y el icosaedro , mientras que el número de aristas se mantiene igual son diferentes Estos pares de sólidos platónicos se denominan sólidos duales .

Podemos convertir un poliedro en su doble, "reemplazando" cada cara con un vértice, y cada vértice con una cara. Estas animaciones muestran cómo:

El tetraedro es dual consigo mismo. Como tiene la misma cantidad de caras y vértices, intercambiarlas no cambiaría nada.

Platón creía que toda la materia en el universo consta de cuatro elementos: aire, tierra, agua y fuego. Pensó que cada elemento corresponde a uno de los sólidos platónicos, mientras que el quinto representaría el universo en su conjunto. Hoy sabemos que hay más de 100 elementos diferentes que consisten en átomos esféricos, no en poliedros.

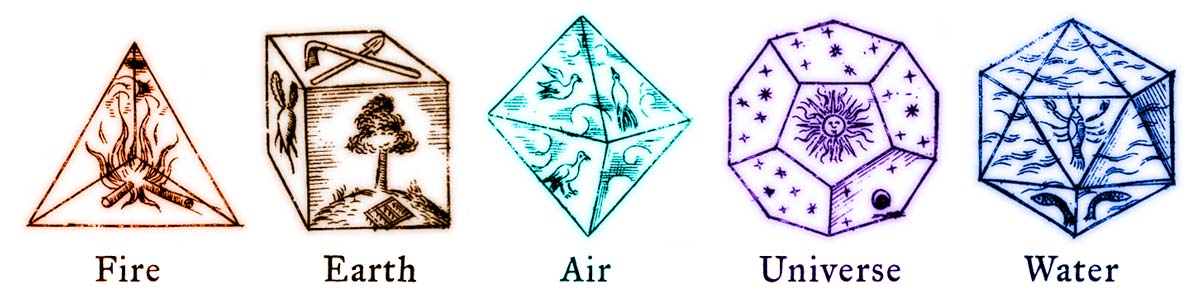
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)

Sólidos Archimedean

Los sólidos platónicos son poliedros particularmente importantes, pero hay muchos otros.

Los sólidos de Arquímedes , por ejemplo, todavía tienen que estar formados por polígonos regulares , pero puedes usar múltiples tipos diferentes. Reciben su nombre de otro matemático griego, Arquímedes de Siracusa , y hay 13 de ellos:

Aplicaciones

Platón se equivocó al creer que todos los elementos consisten en sólidos platónicos. Pero los poliedros regulares tienen muchas propiedades especiales que los hacen aparecer en otras partes de la naturaleza, y podemos copiar estas propiedades en ciencia e ingeniería.