Secuencias y patronesSecuencias aritméticas y geométricas

En 1682, el astrónomo Edmond Halley observó un fenómeno inusual: un objeto blanco brillante con una larga cola que se movía a través del cielo nocturno. Era un cometa, una pequeña roca helada que vuela por el espacio, dejando un rastro de polvo y hielo.

Halley recordó que otros astrónomos habían observado cometas similares mucho antes: uno en 1530 y otro en 1606. Observe que la brecha entre dos observaciones consecutivas es la misma en ambos casos: años.

Imagen del cometa Halley, tomada en 1986 en la isla de Pascua.

Halley concluyó que las tres observaciones eran en realidad el mismo cometa, que ahora se llama cometa Halley. Está orbitando alrededor del sol y pasa la Tierra aproximadamente cada 76 años. También predijo cuándo sería visible el cometa nuevamente:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

En realidad, el intervalo de tiempo no siempre es exactamente 76 años: puede variar en uno o dos años, ya que la órbita del cometa es interrumpida por otros planetas. ¡Hoy sabemos que los antiguos astrónomos observaron el cometa Halley desde el año 240 antes de Cristo!

Dependencias del cometa Halley a lo largo del tiempo: una tableta babilónica (164 a. C.), un tapiz medieval (1070), una revista científica (1910) y un sello soviético (1986).

Un grupo diferente de científicos está investigando el comportamiento de una pelota de tenis que rebota. Dejaron caer la pelota desde una altura de 10 metros y midieron su posición con respecto al tiempo. Con cada rebote, la pelota pierde algo de su altura original:

Los científicos notaron que la pelota pierde el 20% de su altura después de cada rebote. En otras palabras, la altura máxima de cada rebote es el 80% de la anterior. Esto les permitió predecir la altura de los rebotes siguientes:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

Definiciones

Si comparamos ambos problemas, podemos notar que hay muchas similitudes: la secuencia del cometa Halley tiene la misma entre términos consecutivos, mientras que la secuencia de rebotes de pelotas de tenis tiene la misma proporción entre términos consecutivos.

Las secuencias con estas propiedades reciben un nombre especial:

Una secuencia aritmética tiene una diferencia constante d entre términos consecutivos.

El mismo número se suma o resta a cada término, para producir el siguiente.

Una secuencia geométrica tiene una relación constante r entre términos consecutivos.

Cada término se multiplica o se divide por el mismo número, para producir el siguiente.

Aquí hay algunas secuencias diferentes. ¿Puede determinar cuáles son aritméticas, geométricas o ninguna, y cuáles son los valores de d y r?

2, 4, 8, 16, 32, 64, …

es , con una relación .

2, 5, 8, 11, 14, 17, …

es , con la diferencia .

17, 13, 9, 5, 1, –3, …

es , con la diferencia .

2, 4, 7, 11, 16, 22, …

es .

40, 20, 10, 5, 2.5, 1.25, …

es , con una relación .

Para definir una secuencia aritmética o geométrica, debemos conocer no solo la diferencia o relación común, sino también el valor inicial (llamado a). Aquí puede generar sus propias secuencias y trazar sus valores en un gráfico, cambiando los valores de a, d y r. ¿Puedes encontrar algún patrón?

Secuencia aritmética

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Secuencia geométrica

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Observe cómo todas las secuencias aritméticas se ven muy similares: si la diferencia es positiva, constantemente, y si la diferencia es negativa, constantemente.

Las secuencias geométricas, por otro lado, pueden comportarse de manera completamente diferente en función de los valores de a y r:

Si , los términos , hasta el infinito. Los matemáticos dicen que la secuencia diverge.

Si , los términos siempre . Decimos que la secuencia converge.

Si , los términos alternarán entre positivo y negativo, mientras que su aumenta.

Aprenderá más sobre convergencia y divergencia en la última sección de este curso.

Fórmulas recursivas y explícitas

En la sección anterior, aprendiste que una fórmula recursiva te dice el valor de cada término en función de los términos anteriores. Aquí están las fórmulas recursivas para secuencias aritméticas y geométricas:

xn=

Un problema con las fórmulas recursivas es que para encontrar el término número 100, por ejemplo, primero tenemos que calcular los 99 términos anteriores, y eso puede llevar mucho tiempo. En cambio, podemos intentar encontrar una fórmula explícita, que nos diga el valor del término n directamente.

Para secuencias aritméticas, tenemos que agregar d en cada paso:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

En el n término, estamos agregando copias de d, por lo que la fórmula general es

xn=a+d×n−1.

Para secuencias geométricas, tenemos que multiplicar r en cada paso:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

En el n término, estamos multiplicando copias de r, por lo que la fórmula general es

xn=a×rn−1.

Aquí hay un resumen de todas las definiciones y fórmulas que ha visto hasta ahora:

y cinco

Una secuencia aritmética tiene el primer término a y la diferencia común d entre términos consecutivos.

Fórmula recursiva: xn=xn−1+d

Fórmula explícita: xn=a+d×n−1

Una secuencia geométrica tiene el primer término a y una relación común r entre términos consecutivos.

Fórmula recursiva: xn=xn−1×r

Fórmula explícita: xn=a×rn−1

¡Ahora echemos un vistazo a algunos ejemplos en los que podemos usar todo esto!

Pay it Forward

Aquí hay un breve clip de la película Pay it Forward, donde Trevor, de 12 años, explica su idea de hacer del mundo un lugar mejor:

La esencia de la idea de Trevor es que, si todos "pagan", una sola persona puede tener un gran impacto en el mundo:

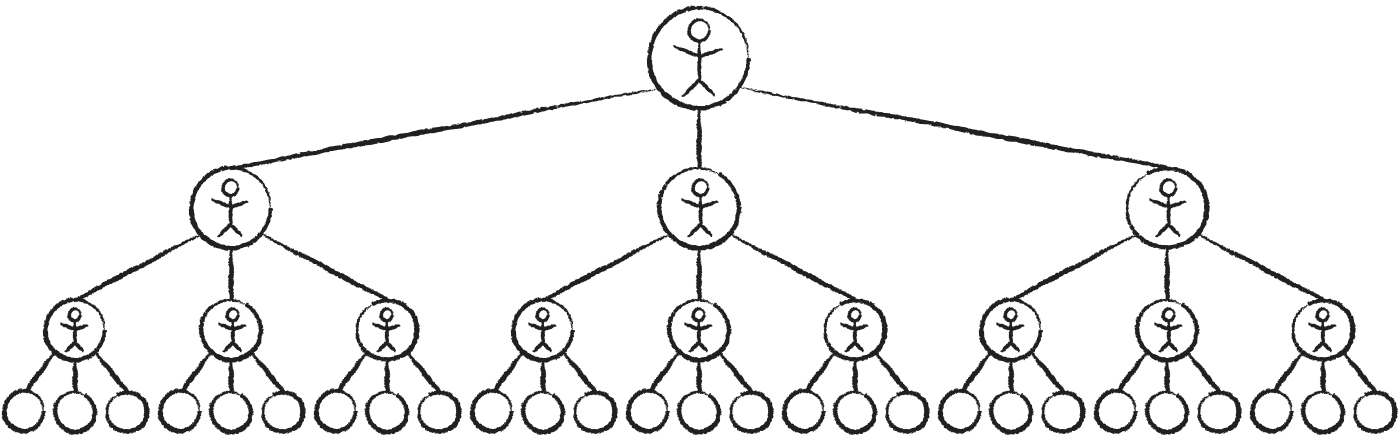
Observe cómo el número de personas en cada paso forma una , con una razón común :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

Usando la fórmula explícita para secuencias geométricas, podemos calcular cuántas personas nuevas se ven afectadas en cualquier paso:

xn =

El número de personas aumenta increíblemente rápido. En el décimo paso, alcanzarías 19,683 nuevos, y después de 22 pasos habrías llegado a más personas que las que actualmente están vivas en la Tierra.

Esta secuencia de números tiene un nombre especial: las potencias de 3. Como puede ver, cada término es en realidad una potencia diferente de 3:

30, 31, 32, {996 }, 34, 35, …

¿Quién quiere ser millonario?

¡MUY PRONTO!

El problema del tablero de ajedrez

¡MUY PRONTO!

Cambiar idioma

Iniciar sesión en Mathigon

Compartir

Restablecer progreso

Glosario