Secuencias y patronesNúmeros de Fibonacci
Imagine que ha recibido un par de conejos, un macho y una hembra. Son conejos muy especiales, porque nunca mueren, y la hembra da a luz a un nuevo par de conejos exactamente una vez al mes (siempre nacen un nuevo par de un macho y una hembra).




















En el mes siguiente tendrías 13 pares de conejos: los 8 del mes anterior, más 5 nuevos grupos de bebés. ¿Puedes detectar un patrón en esta secuencia?
El número de conejos en un mes en particular es
¿Puedes calcular la cantidad de conejos después de unos meses más?
1, 1, 2, 3, 5, 8,
Entonces, después de 12 meses, ¡tendrás 144 pares de conejos!
Esta secuencia de números se llama
Cuando Fibonacci nació en 1175, la mayoría de las personas en Europa todavía usaban el
Cuando regresó a Italia, Fibonacci escribió un libro llamado Liber Abaci (en latín, "El libro de los cálculos"), donde presentó por primera vez los nuevos números arábigos a los comerciantes europeos. Fueron un éxito inmediato, y todavía los usamos hoy.
En una de las páginas de su libro, también investigó los patrones de reproducción de los conejos, por eso los números de Fibonacci llevan su nombre.
Páginas de Liber Abaci de Fibonacci
Por supuesto, los números de Fibonacci no son cómo se reproducen los conejos en realidad en la vida real. Los conejos no tienen exactamente una descendencia macho y una hembra cada mes, y no hemos tenido en cuenta que los conejos mueran eventualmente.
Pero resulta que hay muchos otros lugares en la naturaleza donde aparecen los números de Fibonacci: por ejemplo, las espirales en las plantas. ¿Puedes contar cuántas espirales hay en cada dirección?
Esta piña tiene
Este girasol tiene 34 espirales en sentido horario y 55 espirales en sentido antihorario.
En ambos casos, los números de espirales son números consecutivos de Fibonacci. Lo mismo es cierto para muchas otras plantas: la próxima vez que salga a un paseo, cuente la cantidad de pétalos en una flor o la cantidad de hojas en un tallo. ¡Muy a menudo encontrarás que son números de Fibonacci!
Por supuesto, esto no es solo una coincidencia. Hay una razón importante por la que a la naturaleza le gusta la secuencia de Fibonacci, de la que aprenderemos más adelante.
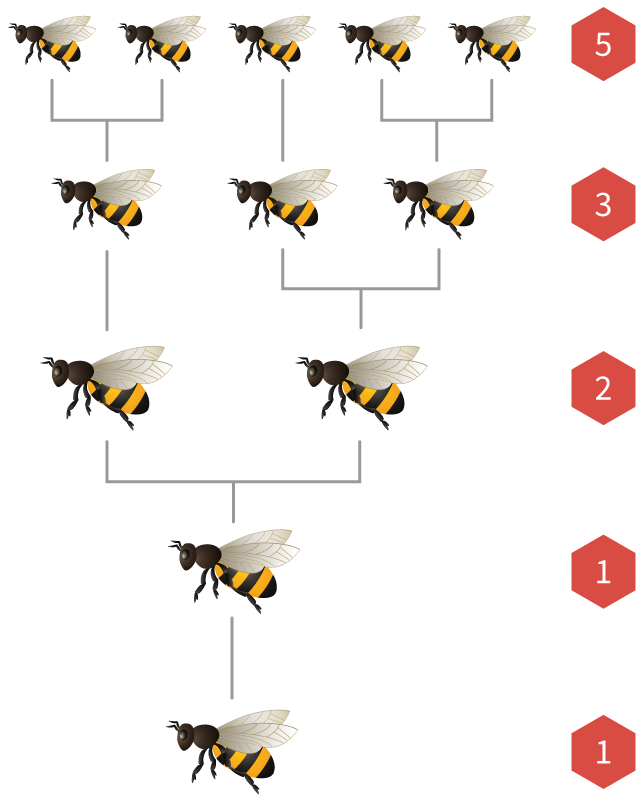
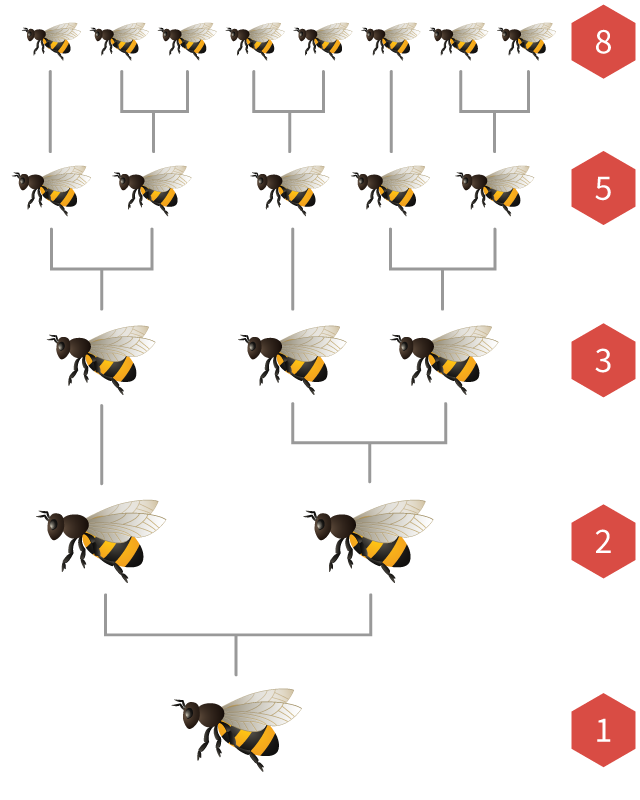
Los números de Fibonacci también aparecen en las poblaciones de abejas melíferas.
En cada colonia de abejas hay una sola reina que pone muchos huevos. Si un huevo es fertilizado por una abeja macho, se convierte en una abeja hembra. Si no se fertiliza, se incuba en una abeja macho (llamada dron).
Esto significa que las abejas hembras tienen
Si dibujamos el árbol ancestral de una abeja, ¡el número de padres, abuelos, bisabuelos y generaciones anteriores siempre son números de Fibonacci!
Ocasionalmente, las abejas jóvenes son alimentadas con una comida especial llamada "jalea real". En ese caso, se convierten en reinas y volarán para comenzar una nueva colmena.
La proporción áurea
Al igual que los
En cada paso, los cuadrados forman un rectángulo más grande. Su ancho y alto son siempre dos números consecutivos de Fibonacci. La proporción del rectángulo es la relación de su ancho y su altura:
Observemos cómo, a medida que agregamos más y más cuadrados, la proporción del rectángulo parece acercarse cada vez más a un número específico alrededor de 1.6. Este número se llama
Mucha gente cree que la proporción áurea es particularmente agradable estéticamente. Es por eso que a menudo la usan artistas y arquitectos, como en estos dos ejemplos:

Se dice que el escultor griego Fidias utilizó la proporción áurea al diseñar el Partenón en Atenas. La primera letra de su nombre,

El sacramento de la última cena, del artista español Salvador Dalí, es una de las muchas pinturas en proporción áurea. En el fondo, también puede ver un gran
Podemos aproximar la proporción áurea entre
Sin embargo, resulta que el valor exacto de
Espirales de Fibonacci
La proporción áurea explica por qué los números de Fibonacci aparecen en la naturaleza, como el cono de girasol y pino que viste al comienzo de esta sección.
Ambas plantas crecen hacia afuera desde su centro (una parte de la planta llamada meristemo). A medida que se agregan nuevas semillas, hojas o pétalos, empujan los existentes más hacia afuera.
Mueve el control deslizante hacia la derecha para visualizar cómo crece una planta. Observe cómo cada hoja se agrega en una rotación diferente a la anterior. El ángulo entre dos hojas consecutivas es siempre el mismo.
Es importante que las flores escojan un ángulo adecuado: las hojas o semillas deben estar aproximadamente a la misma distancia para que obtengan la mayor cantidad de luz solar y nutrientes. En el diagrama a continuación, puede explorar cómo se vería un girasol con diferentes ángulos entre sus semillas:
Podemos recordar que las proporciones de números consecutivos de Fibonacci se acercan cada vez más a la proporción áurea, y es por eso que, si contamos el número de espirales en una planta, a menudo encontraremos un número de Fibonacci.
Es importante recordar que la naturaleza no sabe acerca de los números de Fibonacci. La naturaleza tampoco puede resolver ecuaciones para calcular la proporción áurea, pero en el transcurso de millones de años, las plantas tuvieron mucho tiempo para probar diferentes ángulos y descubrir la mejor opción.
Las plantas y los animales siempre quieren crecer de la manera más eficiente, y es por eso que la naturaleza está llena de patrones matemáticos regulares.
Fibonachos
Hasta ahora, hemos usado la ecuación recursiva para los números de Fibonacci. En realidad, también hay una ecuación explícita, pero es mucho más difícil de encontrar:
Podríamos intentar elegir diferentes puntos de partida para los números de Fibonacci. Por ejemplo, si comenzamos con 2, 1, … en lugar de 1, 1, … obtenemos una secuencia llamada números de Lucas.
Resulta que, independientemente de los dos números iniciales que elijamos, las secuencias resultantes comparten muchas propiedades. Por ejemplo, las proporciones de términos consecutivos siempre
Existen muchos otros acertijos, patrones y aplicaciones relacionados con los números de Fibonacci. Aquí hay algunos ejemplos, que puede probar usted mismo:
Problema
1. Divisibilidad de Fibonacci
(a) ¿Qué números de Fibonacci son pares? ¿Hay un patrón para ubicarlos a lo largo de la secuencia? ¿Puedes explicar porque?
(b) ¿Qué números de Fibonacci son divisibles por 3 (o divisibles por 4)? ¿Que notaste?
2. Sumas de Fibonacci
¿Qué sucede si sumas tres números consecutivos de Fibonacci? ¿Puedes explicar porque?
3. Escaleras de Fibonacci
Al subir las escaleras, puedo dar pasos individuales o saltar dos pasos a la vez. Esto significa que hay muchas posibilidades diferentes de cómo subir una escalera. Por ejemplo, si hay 5 pasos, tengo 8 opciones diferentes:
¿Cuántas opciones hay para escaleras con 6, 7 u 8 escalones? ¿Puedes detectar un patrón? ¿Y cómo se relaciona esto con los números de Fibonacci?
© FoxTrot, by Bill Amend